Kim Seon Deok
[논리회로] 4. 조합논리 본문
4.1 조합회로의 정의
논리회로에는 조합형과 순차형이 있다.
조합형 : 현재 들어오는 입력값에 대해 출력을 결정한다.
순차형 : 조합형 + 저장장치. 저장장치가 출력에 연결되어 입력에 영향을 주는 feedback loop회로이다. 따라서 시간 순서에 따른 입력값과 저장된 내부 상태값에 따라 출력이 달라진다.
조합회로 : 논리게이트의 연결로 이루어진다. 조합논리 게이트는 입력신호에 의해 출력을 만든다.
ex) 레지스터가 조합게이트와 같이 사용되면 전체적으로 순차회로라 볼 수 있다.

4.2 조합회로의 분석(analysis)과정
1.논리도
2.불함수
3.진리표 / 카르노맵
4.회로동작 설명
5.간략화가 끝나면 논리도를 개선
4.3 조합회로의 설계과정
실제 설계과정에서는 게이트의 수, 게이트에 대한 입력의 수, 게이트를 통과하는 신호의 전파시간, 상호 연결 수, 각 게이트의 구동능력의 한계 등의 설계 제약 조건을 고려해야 한다.
1.필요한 입출력 갯수 구하고 기호 지정
2.진리표
3.카르노맵으로 각 출력에 대한 간략화된 불함수를 구함
4.논리도
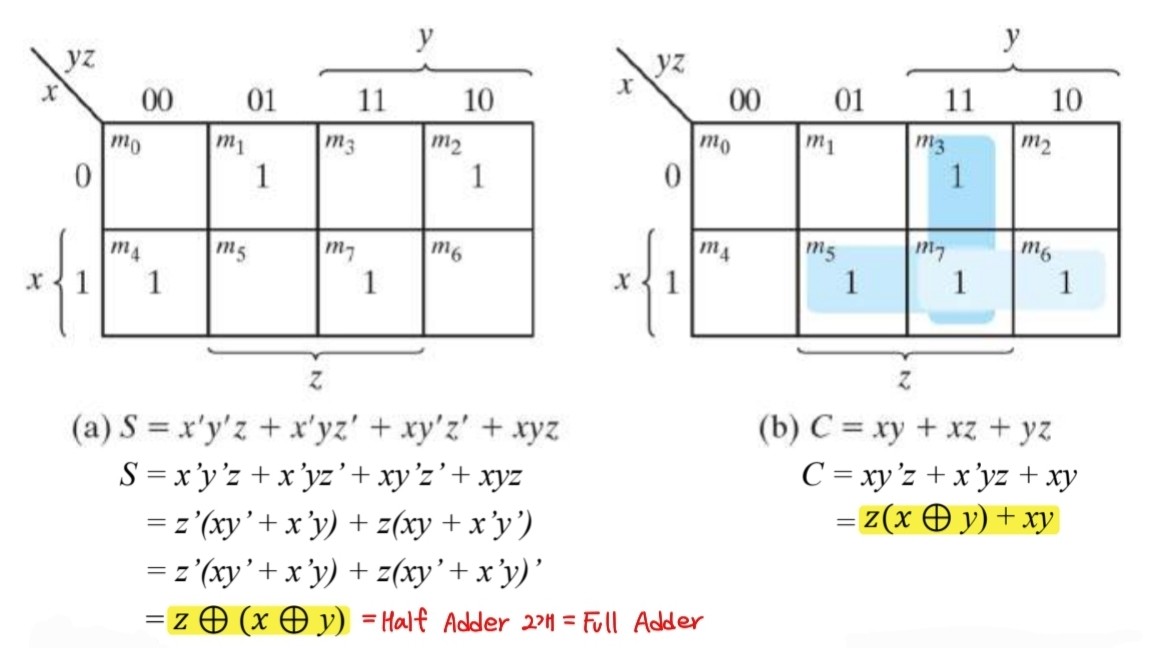
4.4 전가산기, 반가산기
2진 가산기 : 2개의 2진숫자를 더하는 것
(0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 10(캐리발생))
반가산기(Half Adder) : 두 비트의 덧셈을 수행하는 조합회로
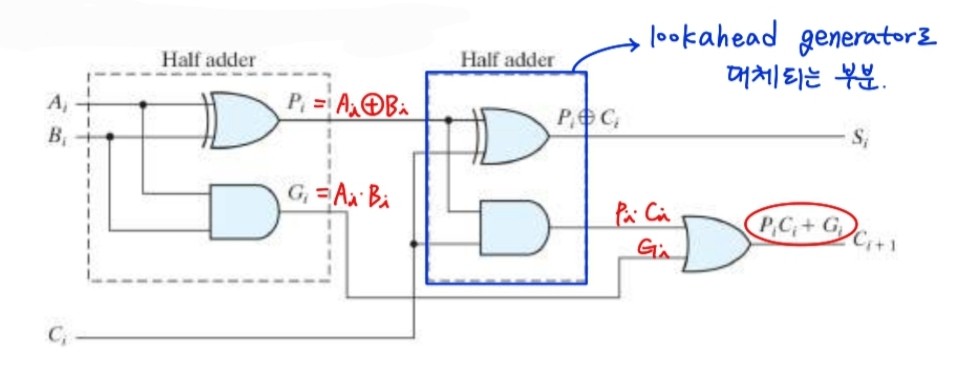
전가산기(Full Adder) : 세 비트의 덧셈을 수행하는 조합회로(두 비트 + 캐리) >> 2개의 반가산기로 구현할 수 있다.
반가산기를 설계한 후 전가산기를 만드는데, n개의 전가산기를 모아, n비트의 숫자를 더하는 가산기(A+B)를 만들 수 있다.
ex) 4비트 : 전가산기 4개
감산기는 보수(A+B프라임)를 이용한다.
반가산기는 입력변수 x,y와 출력변수 s(sum),c(carry)로 구성된다.
두 비트의 덧셈을 수행하는 반가산기의 진리표는 다음과 같다.


sum,carry를 논리게이트로 표현하면 다음과 같다.

sum은 하나의 XOR게이트로, carry는 하나의 AND게이트로 표현해, 전체적인 반가산기는 1-level로 간략화 할 수 있다.
하나의 전가산기는 3비트의 2진숫자의 덧셈을 수행한다. 최하위 비트(LSB)부터 순차적으로 덧셈을 수행하는데, 이 때 해당 자리 두 비트와 이전 자리에서 올라온 캐리를 고려해주어야 한다.


sum,carry를 카르노맵으로 표현하면 다음과 같다.
3비트 전가산기의 sum은 XOR을 두 번 한 것과 같기 때문에 반가산기 2개를 사용하면 된다.

하나의 전가산기는 2개의 반가산기로 구성된다.
즉 n비트를 덧셈하려면 n개의 전가산기를 사용하거나, (n-1)개의 전가산기의 1개의 반가산기를 사용하면 된다.
4.5 2진 가산기
2진 가산기는 첫번째 단의 전가산기의 캐리출력을 다음 단의 전가산기의 입력으로 연결시킨 cascade 구조이다.
다음은 4개의 전가산기로 구성된 4비트 덧셈기이다.
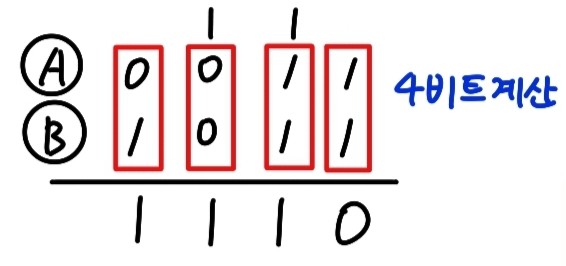

4개의 전가산기가 cascade구조로 연결되어있다.
C0는 보통 0인 경우가 있으므로 맨 처음 전가산기는 반가산기로 대체할 수 있다.
이전 전가산기의 출력캐리는 다음 전가산기의 입력캐리에 연결되어 점점 퍼져나가는 물결형태의 리플 캐리 가산기 구조를 이룬다.
c3를 구하려면 c2,c1,c0를 알아야 하므로 덧셈은 순차적으로 이루어고, 캐리가 자주 발생할 수록 시간지연이 크게 발생한다.
신호는 뎃셈출력을 만들기 위해 여러 게이트들을 통과해야 한다.
전체 신호 전파시간 = 게이트의 전파지연 * 통과해야 하는 게이트 단계의 수
위의 4비트 덧셈기에서 각 게이트마다 10us만큼의 시간지연이 발생한다 가정하면
전체 신호 전파시간 = 4 * 10us = 40us이다.
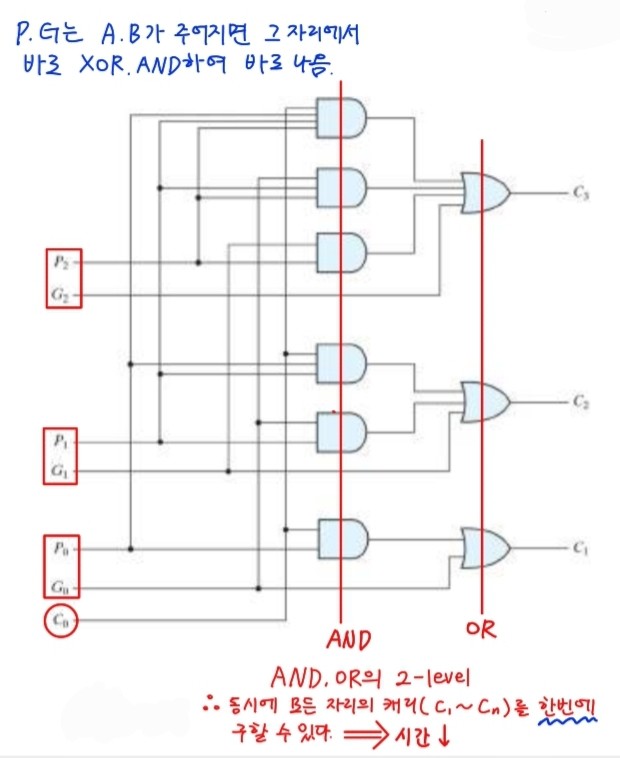
캐리 룩어헤드(carry lookahead logic)의 원리
위의 4비트 전가산기 그림에서 전체 전가산기를 거치지 않고 C0,A0,B0,A1,B1만 가지고 C2캐리를 미리 계산하는 방식이다. 입력캐리 Ci로부터 출력 캐리 C(i+1)에 이르는 신호는 AND와 OR게이트를 통해 전파하는데, 2개의 게이트 레벨을 가진다. 즉 n비트의 가산에서는 캐리가 입력에서 출력까지 전파되기 위해 2n개의 게이트 레벨을 가진다.
따라서 추가적인 회로의 복잡도가 증가하지만 ,전체 전가산기를 거치지 않으면서 c0~c(i-1)을 구하지 않아도, Ci를 구할 수 있어( = 모든 자리의 캐리를 한번에 구할 수 있다.) 전체 신호 전파시간을 감소시키는 원리이다.


4.6 이진 감산기
A - B는 B의 2의 보수를 A에 더하여 계산한다. 2의 보수는 1의 보수에 1을 더한 것이므로, 1의 보수를 인버터로 구현하고 입력캐리를 통해 합에 1을 더하면 된다.
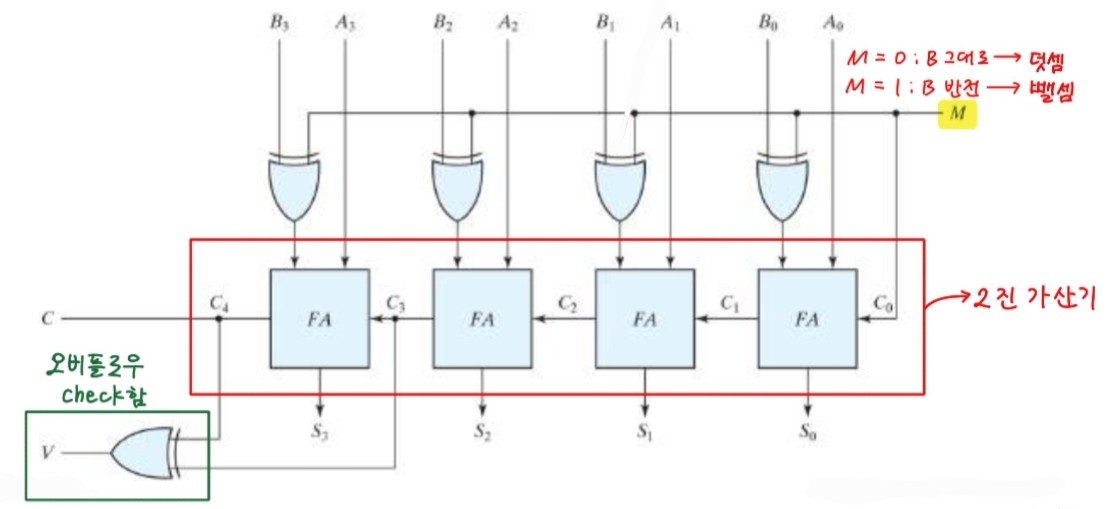
이진 감산기는 이전의 4비트 가산기에서 4번의 입력마다 XOR게이트가 추가되었고 입력M, 맨 끝단의 XOR게이트가 추가된 형태이다.
M = 0이면 XOR게이트를 통해 B가 그대로 출력되어 덧셈의 기능을 수행
M = 1이면 XOR게이트를 통해 B'이 출력되어 뺄셈의 기능을 수행
맨 끝단의 XOR게이트는 오버플로우를 감지한다.
부호가 없는 수(unsigned number)의 경우
A >= B 이면 A - B
A < B 이면 B - A의 2의 보수
부호가 있는 경우(signed number)에는 오버플로우에 주의해야 한다.
오버플로는 n비트의 두 수를 더해서 n+1의 자리를 차지할 때 발생하는 것이다.
부호가 없는 수가 더해질 때 오버플로는 최상위 비트의 캐리출력에서 감지된다.
부호가 있는 수가 더해질 때에는 최상위 비트가 부호이므로 음수는 2의 보수형태이다. 따라서 부호비트는 수의 일부분이고 최종캐리는 오버플로가 아니다.
이 때 오버플로는 (양수 + 양수) 또는 (음수 + 음수)일 때 발생한다.

오버플로 상태는 부호비트 자리에 들어가는 캐리와 부호비트 자리에서 발생하는 캐리출력을 보면 알 수 있다.
이 두 캐리가 다르면 오버플로이고, 두 캐리를 가산기의 맨 끝단에 있는 XOR게이트에 통과시켜 1이면 오버플로로 판단한다.
4.7 10진 가산기
BCD코드는 10진수 각 자릿수를 2진수형태로 변환한 것으로 두개의 BCD코드를 더하면 19(9 + 9 + 1)보다 클 수 없다.
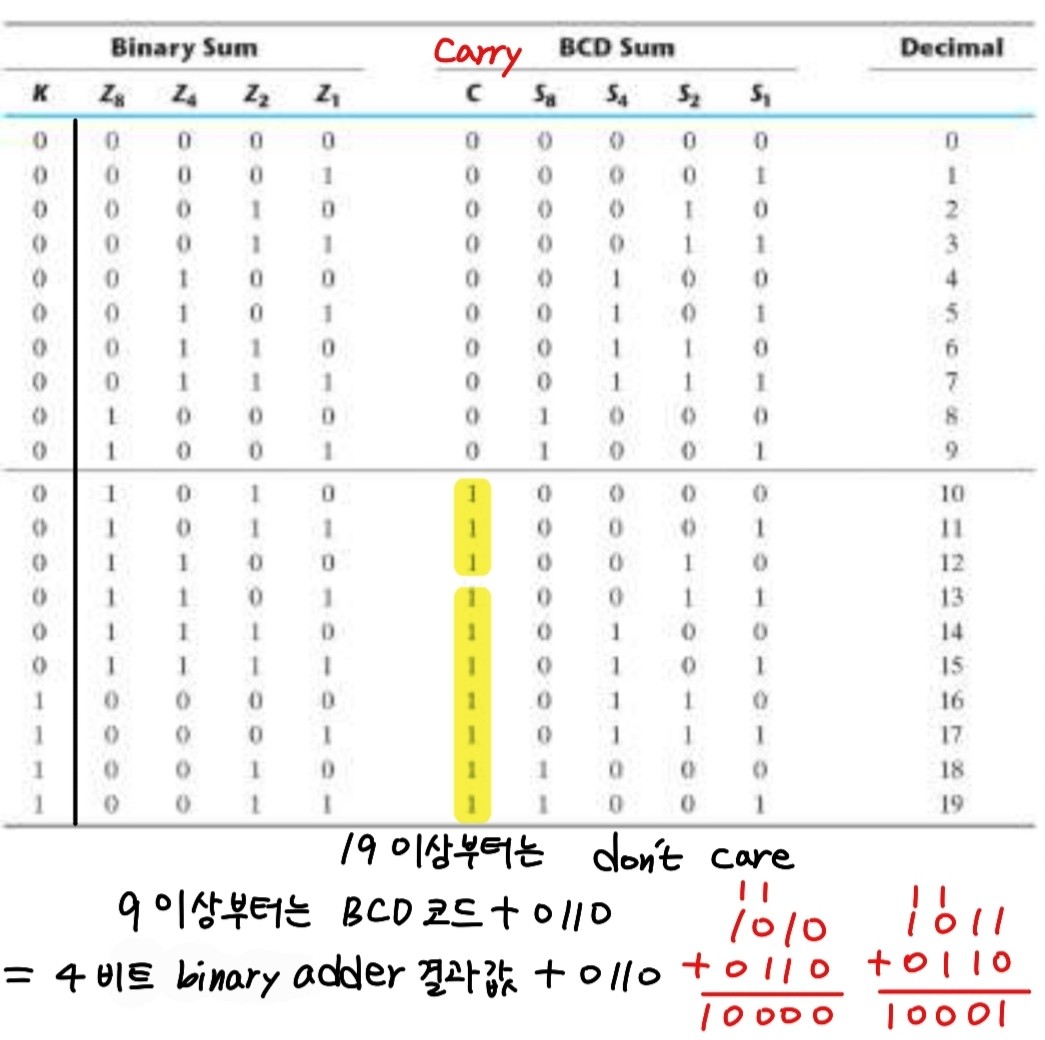
Z1,Z2,Z4,Z8의 Binary sum이 입력일 때 S1,S2,S4,S8,C가 출력된다.
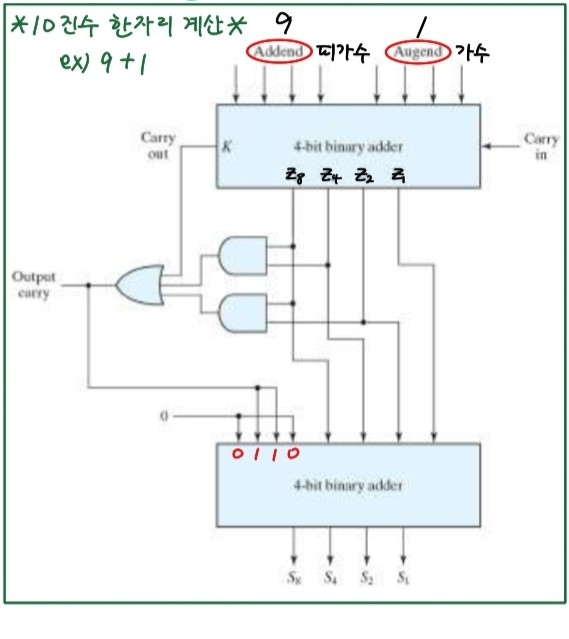
예를 들어 9 + 1의 상황이라면 9와 1을 각각 BCD코드로 바꾼 이진수 4 + 4 = 8 비트가 입력으로 들어간다.
이 때 Sum값이 10 이상이면 캐리가 발생하게 되는데, 이때부터는 BCD코드로 나타기 위해선 binary adder 결과값에 0110을 더해주어야 한다.(BCD코드 + 0110)
4.8 2진 곱셈기


A0B1,A0B0,A1B1,A1B0은 AND게이트로 곱하고 반가산기를 통해 곱셈에서 겹치는 부분을 더해준다.

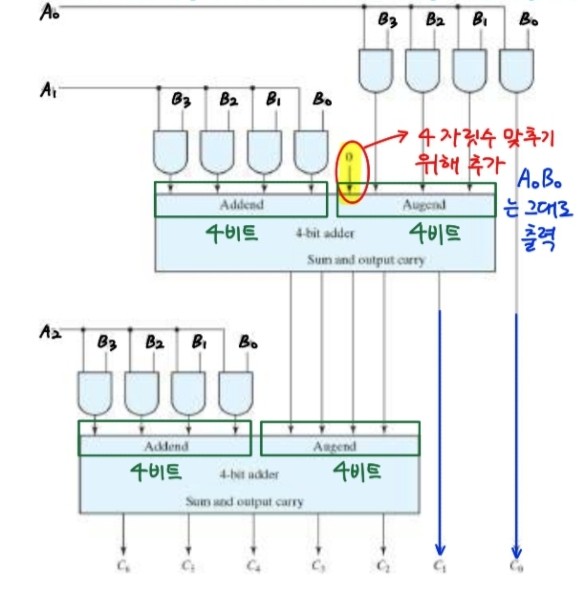
따라서 가산기, 감산기, 곱셈기는 Adder로 해결할 수 있다.
4.8 비교기
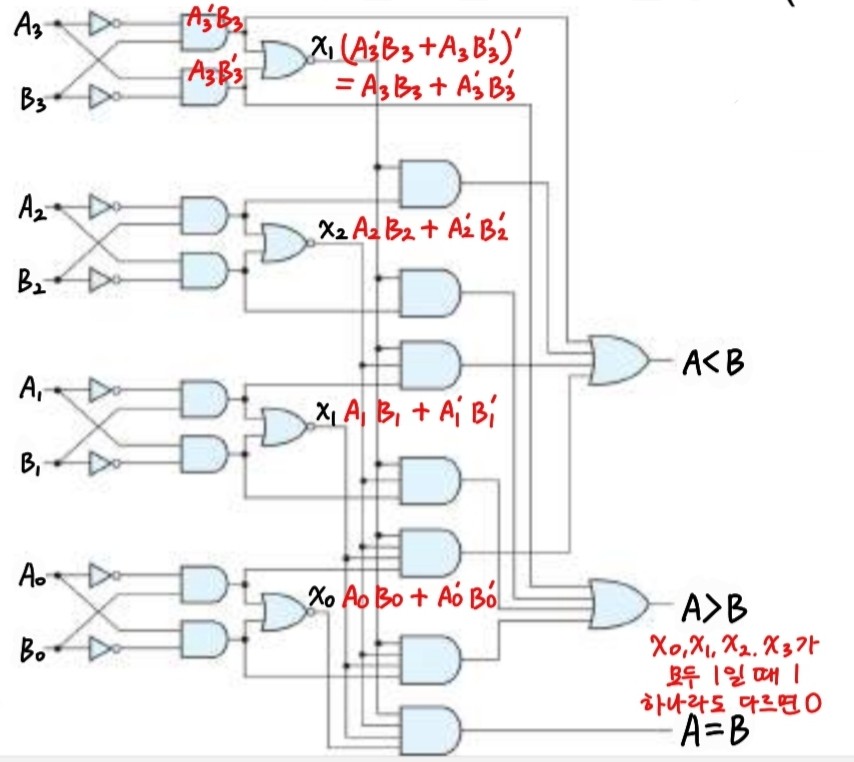
4비트 비교기의 경우 4쌍의 A,B를 비교한다. 아래의 그림에서 x0,x1,x2,x3이 모두 1이면 A = B.
x0,x1,x2,x3중 어느 하나라도 0이라면 (A3,A2,A1,A0)(B3,B2,B1,B0)의 MSB부터 LSB 순으로 값을 비교하여 같지 않은 숫자쌍에 도달할 때 A가 1, B가 0이면 A>B. A가 0, B가 1이면 A<B로 판단한다.
4.9 디코더
디코더는 n개의 입력을 2^n개의 출력으로 변환하고 그 중 하나를 선택한다.

3 to 8 디코더는 3개의 입력변수로부터 2^3개의 최소항을 만들고 그 중 한개를 선택하여 출력을 1로 내보낸다.

n to m 디코더는 n개의 입력변수로부터 2^n(=m)개의 최소항을 만들고 그 중 한개를 선택하여 출력을 1로 내보낸다.
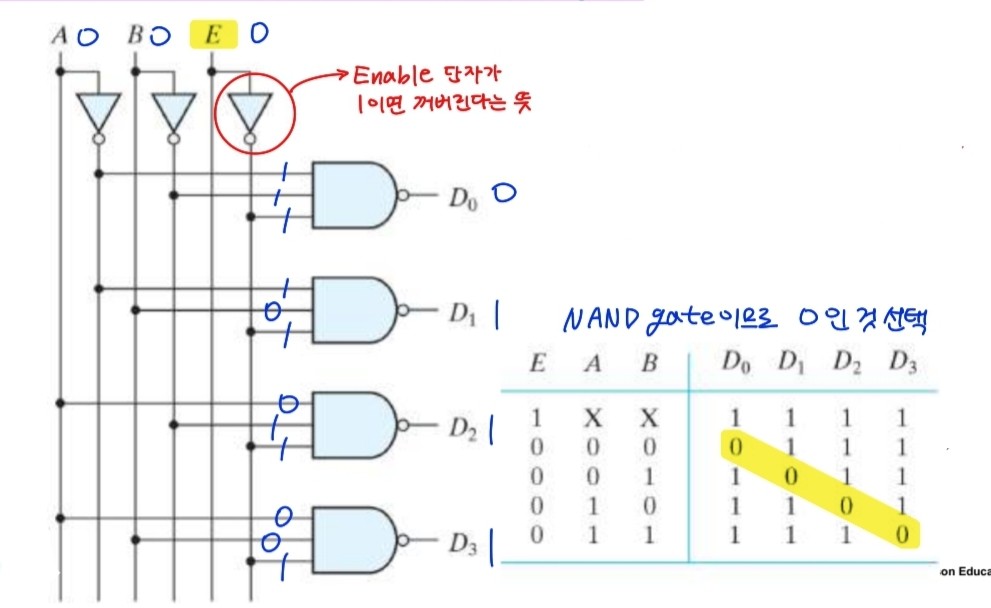
위의 그림은 2 to 4 디코더에 enable단자가 추가된 모습이다. 또한 이전 디코더와는 다르게 출력 이전 AND게이트 대신 NAND게이트를 사용했다. 따라서 enable단자가 1이면 A,B값에 상관없이 디코더가 동작하지 않고
enable 단자가 0이면 A,B값에 따라 출력이 0으로 한 개씩 나오게 된다.

3 to 8 디코더를 2개 이용한 4 to 16디코더에서 w단자는 enable 단자이다. enable단자가 0이면 위쪽 3 to 8 디코더가 동작하고, enable단자가 1이면 아래쪽 3 to 8 디코더가 동작한다.

디코더는 n개의 입력으로 2^n개의 최소항을 제공하므로, 디코더와 OR게이트를 연결하면 반가산기나 전가산기의 sum과 carry에 대한 진리표와 불함수를 작성했던 것 처럼 같은 결과를 얻을 수 있다.
4.10 인코더
인코더는 디코더와 반대되는 디지털 회로이다. 2^n개의 입력과 n개의 출력을 가진다.
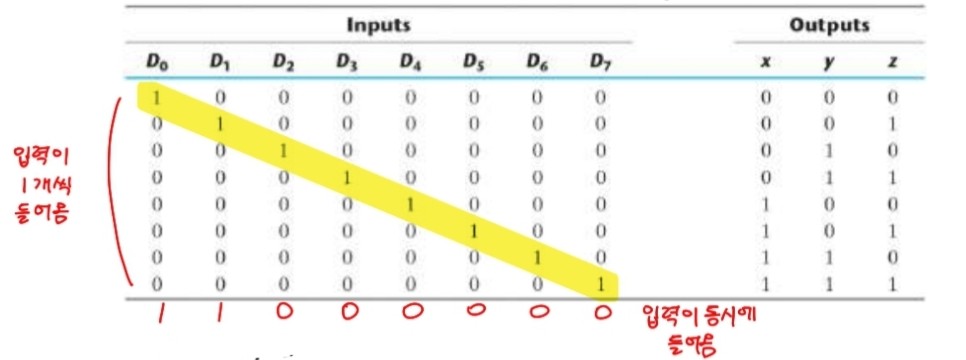
8 to 2 인코더에서 입력은 8개이고 입력조합은 모두 2^8개이다. 위의 진리표에서는 입력이 동시에 들어오는 경우는 제외하고 한 개의 입력만 들어오는 경우(10000000)만 나타내었는데, 만약 입력이 동시에 들어오는 경우라면(11000000) 각 입력마다 우선순위를 부여한다.

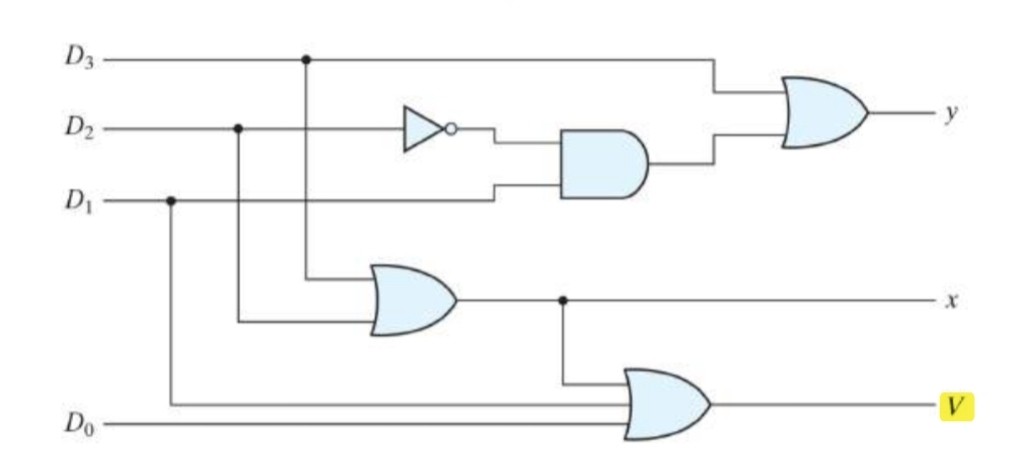
우선순위를 부여한 4 to 2 인코더의 진리표이다. 입력은 4개이고 입력조합은 모두 2^4개이다. 이 때 추가된 출력 v 는 verification의 약자로, v = 0이면 출력이 무효하다. 하지만 v = 1이면 출력이 유효해져, 우선순위에 따라 출력을 매기게 된다.
4.11 멀티플렉서
많은 입력 중에서 하나의 2진 정보를 선택하여 출력으로 연결한다.
2^n개의 입력과 n 개의 selective 신호, 1개의 출력으로 구성된다.
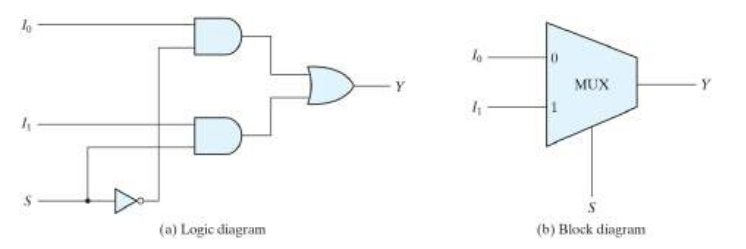
디코더와 멀티플렉서 같은 경우 아주 비슷하다.
디코더는 입력의 조합에 따라 출력의 값을 0 또는 1 로 선택한다. 입력이 n개면 출력은 2^n개 중 하나이다.
멀티플렉서는 selective bit를 이용해 입력값들 중 1개를 선택해 다이렉트로 출력을 선택된 입력값 1개를 내보낸다.
출력의 형태는 선택된 하나의 입력값 형태와 같으며 반드시 0 또는 1이 아닐 수 있다. 입력이 2^n개면 그 중 하나를 선택해서 내보낸다.
멀티플렉서에서 입력값이 주어지긴 하지만, selective bit는 실질적으로 사용자가 조절할 수 있는 입력값이다. 따라서 selective bit를 통해 I0~I3 중 하나를 결정해 출력으로 결정된 기존 입력값을 그대로 내보내는 것이다.
멀티플렉서의 이러한 특성을 통해 data selector라고도 한다.


quadruple 2 to 1 멀티플렉서 같은 경우 입력단자가 A0~A3, B0~B3, Enable단자로 구성되어 있는데,
Enable 단자가 1이면 멀티플렉서 전체가 동작하지 않고, Enable 단자가 0이고 Selective 단자가 0이면 A0~A3단자 4비트들이 동작한다. Enable 단자가 0이고 Selective 단자가 1 이면 B0~B3단자 4비트들이 동작한다.
전체 8 비트 중 4비트씩 데이터를 다중으로 동작시킬 수 있으므로 quadruple이 붙은 것이다.
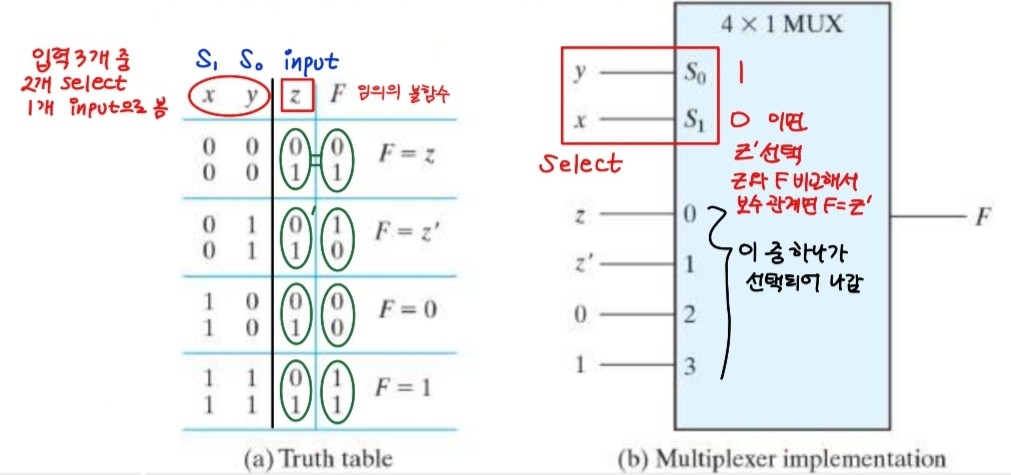
위 그림은 4 to 1 멀티플렉서의 진리표이다. 주어진 진리표에서 입력 x,y는 selective 단자 역할을 하고 z는 기존 입력 역할을 한다. x,y가 각각 0, 1 일 때 z가 f와 같으면 z에 해당되는 0이 출력되고, z가 f와 보수관계이면 z'에 해당되는 1이 출력된다.

8 to 1 멀티플렉서 또한 selective 단자 A,B,C 그리고 기존 입력 D로 구성되는데, A,B,C에 따라 D와 F를 비교하여 그에 해당되는 값을 F로 출력한다.
디멀티플렉서
디멀티플렉서는 멀티플렉서의 반대이다. 입력이 1개이고 출력은 2^n개 중 1개이다.
3상태 게이트

멀티플렉서는 3-상태 게이트로 구성될 수 있다.
여기서 3 상태는
1. 1
2. 0
3. 끊어짐( = High - Z)
버퍼에서 control line이 추가되었는데, C = 1이면 입력 A가 그대로 출력 Y로 통과된다. 이 때 A가 1이면 Y는 1이고, A가 0이면 Y는 0이다. C = 0이면 입력에서 출력으로 가는 회로가 끊어져 개방회로가 되는데, 이 때 임피던스가 매우 커진다.

3상태 게이트는 멀티플렉서와 디코더에 함께 사용되어 출력을 조절하는 데 이용될 수 있다.
'논리회로' 카테고리의 다른 글
| [논리회로] 6. 레지스터와 카운터 (0) | 2022.10.23 |
|---|---|
| [논리회로] 5. 동기식 순차 논리 (0) | 2022.10.17 |
| [논리회로] 3. 게이트 레벨 최소화 (0) | 2022.10.12 |
| [논리회로] 2. 부울 대수와 논리 게이트 (0) | 2022.10.10 |
| [논리회로] 1. 디지털 시스템과 2진수 (0) | 2022.10.10 |




