Kim Seon Deok
[논리회로] 1. 디지털 시스템과 2진수 본문
1.1 디지털 시스템
사람의 손가락은 10개이다. 사람이 사용하는 수는 10진수이다.
컴퓨터가 사용하는 수 체계는 0과 1의 이산적인 수로 이루어진 2진수(binary)이다. 이를 디지털 시스템이라 한다.
디지털 시스템은 2진수 형태로 나타나는 정보의 이산적 요소를 처리하는 시스템이다.
디지털 시스템의 예로 컴퓨터가 있다. 컴퓨터 내부를 이루는 모든 장치는 0과 1에 의해 작동한다.
(하드디스크, SSD : 오랜 기간 동안 보관 목적, RAM : 임시저장장치)
그 중 CPU는 프로그램에 따라 산술 및 기타 데이터 처리 작업을 진행하고, 메모리는 프로그램과 데이터를 저장한다.
비트(bit, binary digit) 라 불리는 2진수는 0과 1을 가진다. 이러한 비트의 집합을 2진 코드(binary code) 라 한다.
1바이트 = 8 비트(2진수 8개)
1.2 2진수 시스템
밑이 2이고 계수에 2의 거듭제곱을 곱함
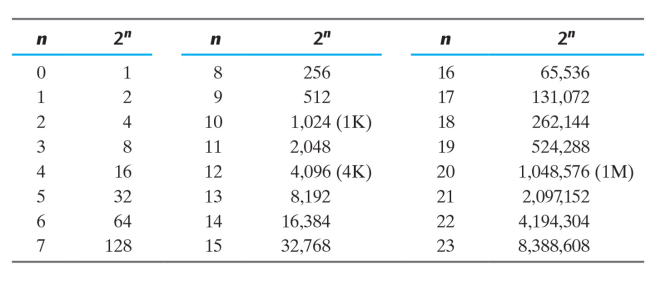
컴퓨터에서 2^10은 K, 2^20은 M, 2^30은 G, 2^40은 T, 2^60은 P.......
10진수를 2로 나누어 몫과 나머지를 이용해 2진수로 변환해 줄 수 있다.
단 10진수의 소수를 2진수로 변환하는 것은 나눗셈 대신 곱셈을 사용하고 나머지 대신 정수를 선택한다.
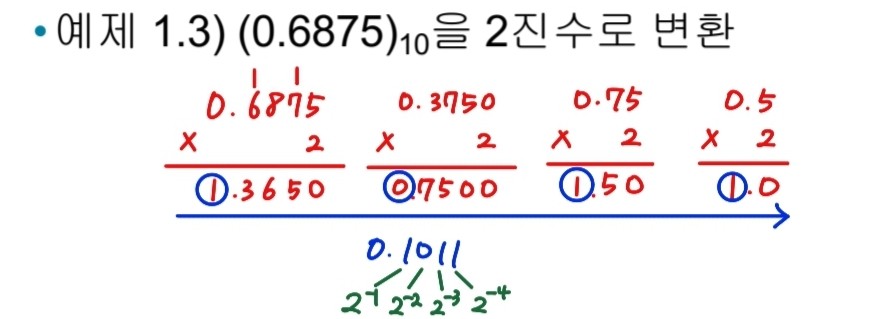
1.3 8진수와 16진수
2진수, 8진수, 16진수는 서로 유사하다.
컴퓨터에서는 2진수의 특성을 가지면서 표시하는 숫자 갯수를 줄이기 위해 8진수나 16진수를 사용한다.
2진수에서 8진수, 16진수로의 변환은 2진수의 숫자를 소수점 기준으로 숫자 3개(8진수), 숫자 4개(16진수)로 묶어서 변환한다.
역으로 8진수에서 2진수로의 변환은 8진수의 숫자를 세 자리 2진수로 변환, 16진수에서 2진수로의 변환은16진수의 숫자를 네 자리 2진수로 변환한다.
16진수 2개는 8bit = 1 byte

8진수 > 16진수 변환 16진수 > 8진수
8진수 - 2진수 - 16진수 16진수 - 2진수 - 8진수
8진수 <> 16진수는 2진수로 변환하는 과정을 거쳐야 한다.
1.4 보수
보수는 컴퓨터에서 덧셈으로 뺄셈 연산을 하고 논리적 조작을 쉽게 하기 위해서 사용한다. 시간과 비용을 절감하기 위한 목적으로 사용한다. 보수의 보수는 원래 수이다.
2진수의 보수
- 2의 보수 : 1으보수로 만들고 1을 더함
- 1의 보수 : 1을 0으로, 0을 1로 뒤집기
10진수의 보수
- 10의 보수 : 9의 보수로 만들고 1 더함
- 9의 보수 : 9.....9에서 해당 숫자 빼기
8진수의 보수
- 8의 보수 : 7의 보수로 만들고 1 더함
- 7의 보수 : 7......7에서 해당 숫자 빼기
보수를 이용한 뺄셈(M-N)
1. 2의 보수를 사용한 방법
- M >= N일 때
M에 N의 2의보수(n)를 더한 것을 더하고 캐리를 버림
- M < N일 때
M의 2의 보수(m)와 N을 더하고 다시 (m+N)2의 보수를 구한 후 -부호를 붙여줌

2. 1의 보수를 사용한 방법
- M >= N일 때
N의 1의 보수를 구하고 M과 더한 후 캐리를 버리고 1을 더함
- M < N일 때
M의 1의 보수를 구하고 N과 더한 후 1의보수를 취한 다음 -를 붙임
- 1의 보수를 사용한 방법
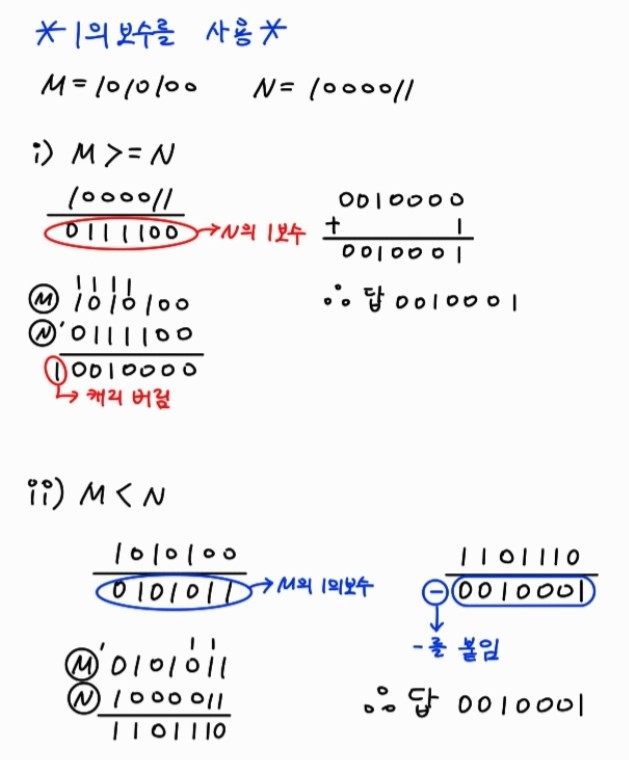
1.5 부호 있는 2진수
부호-크기 방식(signed magnitude convention) : 숫자의 가장 왼쪽 비트를 부호, 나머지 비트를 숫자로 나타낸다.
양수는 0, 음수는 1로 함
11001은 부호가 없는 수로 간주하면 25, 부호가 있는 수로 간주하면 -9
부호-보수 방식(signed-complement system) : 음수를 보수로 표현.
양수는 가장 왼쪽 비트가 0, 그 보수는 음수를 나타내는 1로 시작
+9 = 00001001
부호-크기 방식 : 10001001
부호화 1의 보수 : 11110110(-9)
부호화 2의 보수 : 11110111(-9)
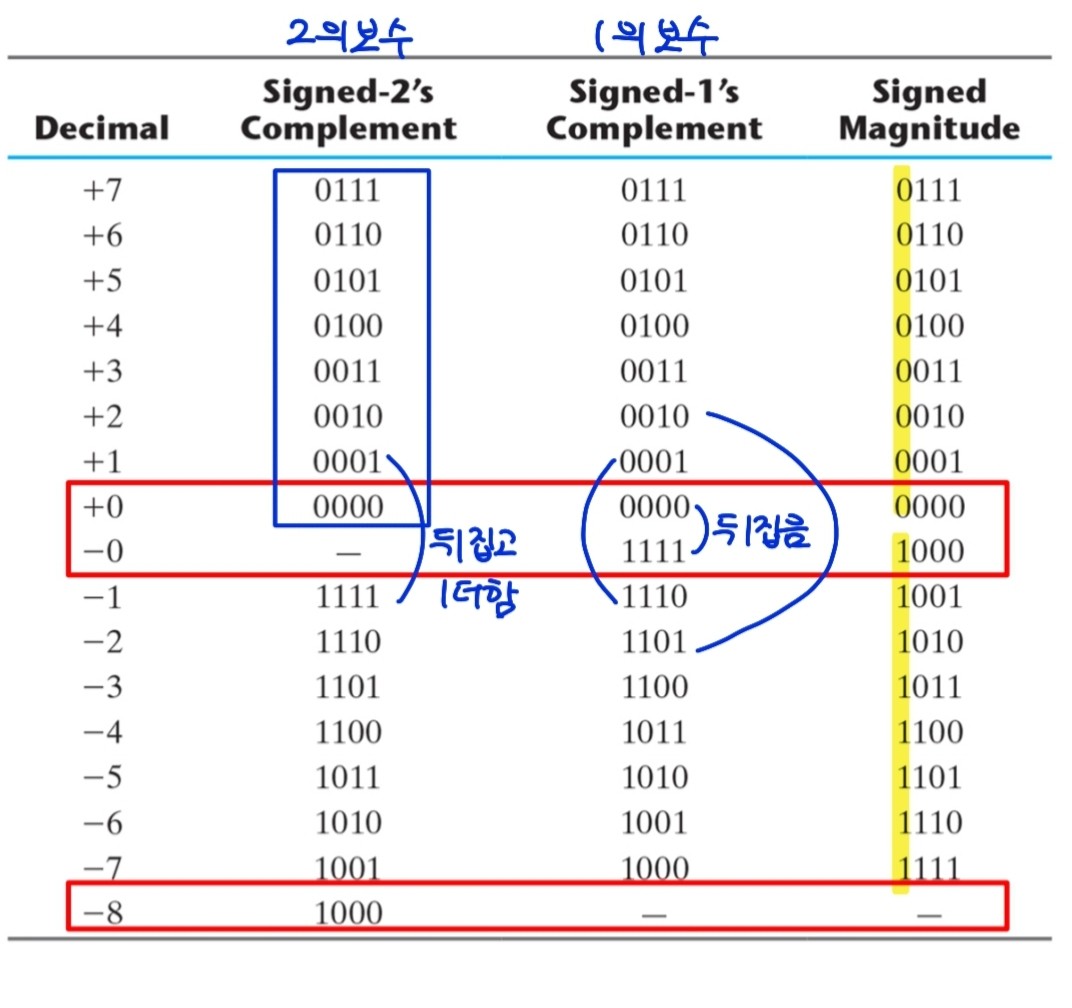
1.6 2진 코드
2진 코드는 2진수와 다른 개념이다.
2진 코드에서 n비트로 2^n개에 해당하는 값을 0과 1로 표현할 수 있다.즉 2진수 n개로 2^n개를 표현할 수 있다.
2진수 시스템이 컴퓨터에 가장 자연스럽지만 사람은 10진수 시스템에 익숙하기 때문에 사람에게 익숙한 10진수를 입력 받아서 컴퓨터에 맞도록 2진수로 변환하고 연산한 다음 결과값을 다시 10진수로 바꾸어서 사람에게 출력한다.
따라서 10진수를 2진코드로 나타낼 필요가 있다.
1.BCD 코드(Binary Coded Decimal)
2진수로 코드화한 10진수이다. 즉 각 자릿수 하나씩을 2진수로 변환한 것으로, 2진수로 변환하는 것과 다른다.
4개의 비트를 사용하여 전체 16개의 조합 중 1~9까지의 10개 사용
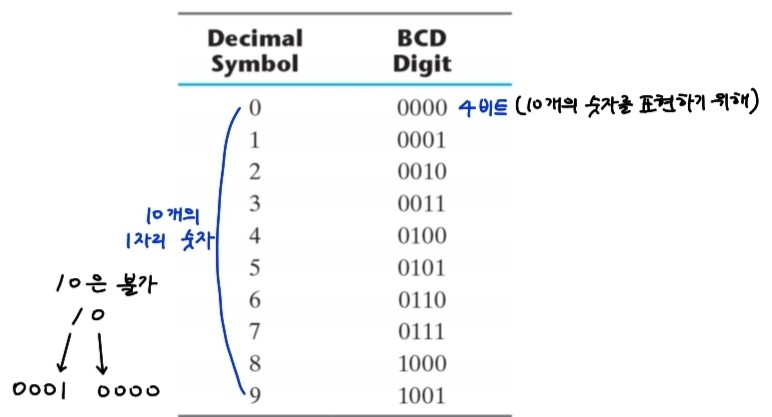
(396)10 >>>> (0011/1001/0110)BCD
BCD코드에도 그밖의 다른 코드들이 존재한다.
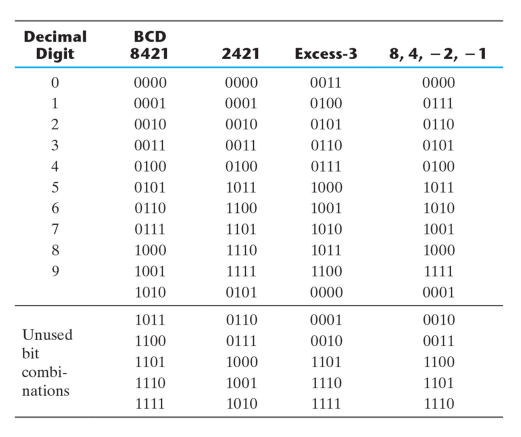
- 2421코드는 각 자릿수가 2,4,2,1을 뜻한다.
ex) 2421코드 0011은 10진수로 변환할 때 0*2 + 0*4 + 2*1 + 1*1 = 3이다.
각 자릿수마다 2,4,2,1이 곱해지므로 BCD코드와 같이 가중코드이다. 또한 자기보완적인 코드이다.
10진수 5를 가중코드로 변환할 때 1011도 가능하고 0101도 가능하다.
10진수 6을 가중코드로 변환할 때 0110도 가능하고 1100도 가능하다.
- Excess-3코드는 BCD코드로 변환한 후 1011(3)을 더해준 것이다. 1011을 더해주므로 자기보완적인 코드이다.
(395)10 = 0110/1100/1000
- 84-2-1코드는 각 자릿수가 8,4,-2,-1을 뜻한다.
01111 = 8*0 + 4 * 1 + -2 * 1 + -1 * 1 = 1
2.그레이 코드
한 숫자에서 다른 숫자로 갈 때 한 비트만 변화하여 숫자가 연속적으로 변화할 때 오류를 줄여준다.
그레이코드는 카르노맵에 이용된다.
7에서 8로 갈 때 0111에서 1100.

3.ASCII문자코드(American Standard Code for Information Interchange)
7비트(128개)를 사용해서 26개의 대문자, 26개의 소문자, 10개의 숫자, 32개의 특수문자, 34개의 제어문자를 표현한다.
확장 ASCII코드: 대부분의 컴퓨터는 8비트가 기본단위이기 때문에 ASCII코드를 사용하면 1비트가 남게 되는데, 남은 1비트는 패리티비트로 사용되어 오류검출에 이용된다.
2^7 = 128 아스키 코드
2^8 = 256 확장 아스키 코드


MSB비트 : 통신에서 오류를 검출하고 이를 줄이기 위한 비트
패리티 비트 : 1의개수가 짝수개이면 even parity bit, 홀수개이면 odd parity bit
1.7 2진 기억 장치와 레지스터
레지스터는 2진셀의 집합이다. 여기서 2진 셀은 2개의 상태(0과 1)를 기억하는 단위를 말한다. 즉 1비트를 저장하는 저장장치이다.
(2진 셀은 하나의 기억 저장 장치의 단위로 전압을 통해 데이터를 저장한다. 0은 방전 1 은 충전을 나타낸다.)
예를 들어, 1100 0011 1100 1001이 16셀의 레지스터에 저장되어 있다면
2진수로 보았을 땐 50121이고 8비트의 문자 2개라면(아스키) CI(11000011 / 11001001. 8개씩 끊음)이며, 3초과코드로 보면 9096(4개씩 끊고 1011을 더함)
컴퓨터가 2진 셀을 다루는 방식
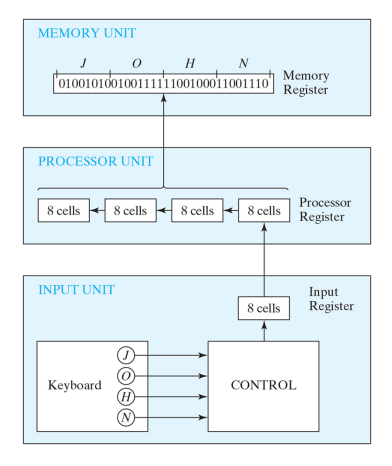
키보드 에서 j,o,h,n,dmf 1글자씩 입력하면 control을 지나 input register를 통해 processing unit으로 8 비트의 아스키값이 순차적으로 이동하고 메모리에 j,o,h,n순으로 각 알파벳의 8비트 값이 저장된다.
binary information processing에서 레지스터
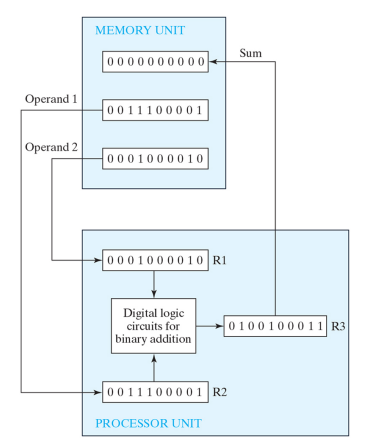
메모리 유닛에 숫자가 저장되어있다 가정하면, operand1, operand2(operand : 연산을 하는 숫자들)가 처음에 메모리에 저장되어 있다가 operand1은 CPU 내 R2에 임시저장되고 operand2은 CPU 내 R1에 임시저장된다.
이후 2진 논리연산 장치에 의해 연산을 수행 후 연산 결과값을 CPU에 임시저장 했다가 메모리 유닛으로 보내고
R1,R2를 비운 후 다음 연산을 수행한다.
1.8 2진 논리
2진 논리란 2진 변수와 논리 연산으로 구성된 것을 말한다.
변수는 A,B,C,x,y,z 등으로 표현하고 각 변수는 0 또는 1을 가진다.
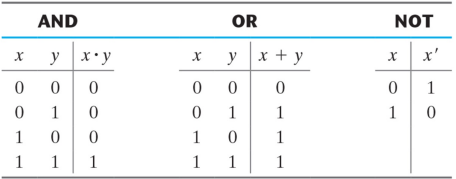
기초 논리 연산은 AND,OR,NOT이며 2진수 연산과 다르다.
(2진수 연산) 1 + 1 = 10 (2진 논리) 1 + 1 = 1
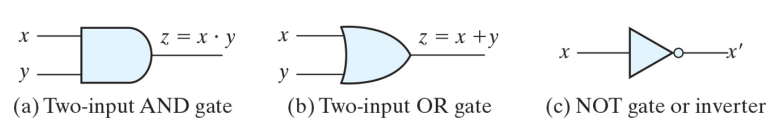
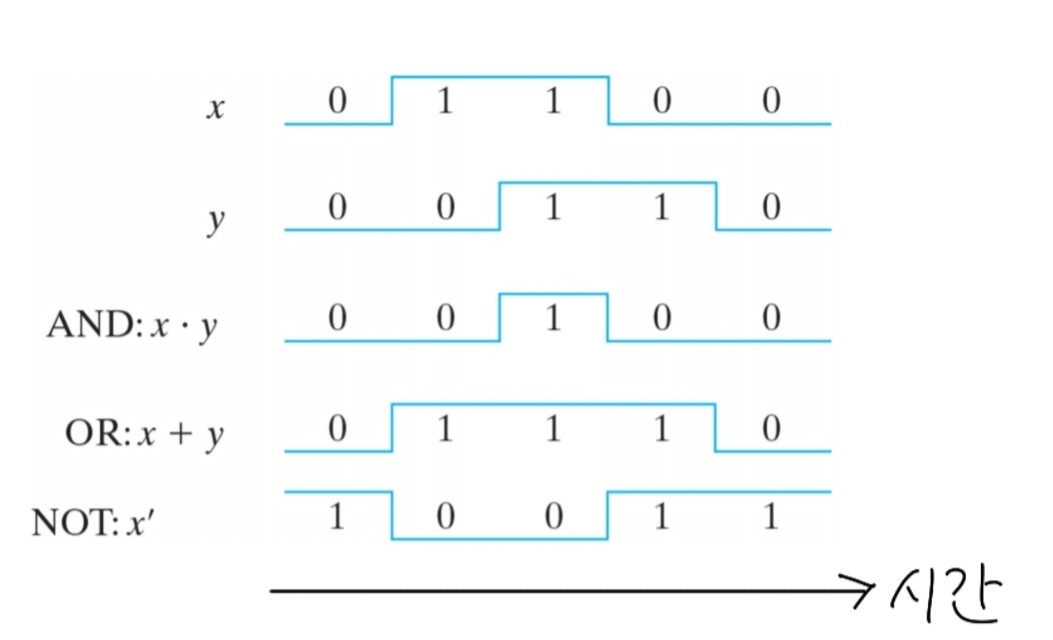
2진논리를 게이트에서 구현할 수 있는데,
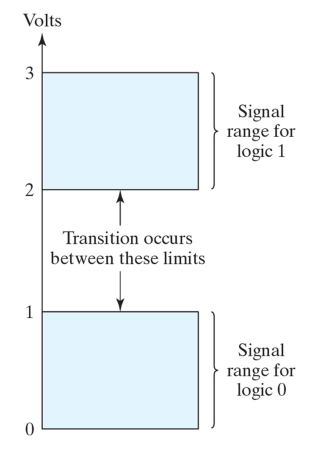
논리 게이트란, 전압과 같은 전기적 신호로 0과 1을 표현하고, 이를 논리연산(AND,OR,NOT) 한 후 다시 전기적 신호로 출력하는 회로이다. 이 때 0과 1을 나타내는 전압값이 필요한데 높은 전압을 1로, 낮은 전압을 0으로 표현한다.
그림과 같이 0~1v는 0으로 2~3v는 1로 할 수 있는데 1~2v 와 같은 중간전압의 경우 매우 애매하다. 이때 transition현상이 발행하고 패리티비트를 이용하여 전압으로 바꾸어 줄 수 있다.
강의 출처
https://www.youtube.com/watchv=4JqExw6DDuo&list=PLP4rlEcTzeFLmvuP6lmWWFQDNHFn0UAkk&index=2
'논리회로' 카테고리의 다른 글
| [논리회로] 6. 레지스터와 카운터 (0) | 2022.10.23 |
|---|---|
| [논리회로] 5. 동기식 순차 논리 (0) | 2022.10.17 |
| [논리회로] 4. 조합논리 (0) | 2022.10.14 |
| [논리회로] 3. 게이트 레벨 최소화 (0) | 2022.10.12 |
| [논리회로] 2. 부울 대수와 논리 게이트 (0) | 2022.10.10 |




