Kim Seon Deok
1. Back propagation 본문
2. Back propagation
Loss를 바탕으로 각각의 w 하나하나가 얼마나 영향을 주었는지 알아내고, 좀 더 적절한 방향으로 w들을 변경해 나가는 것
-학습의 목표 : 가능한 작은 loss 값을 갖는 w를 찾는 것 > 작은 loss & 좋은 w
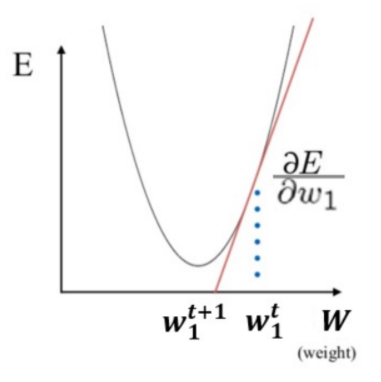
-w와 loss의 관계를 이용해 좋은 w를 찾아가는 방법 : 그래프의 기울기를 이용한 (경사 하강법) > 그래프의 최저점을 찾음
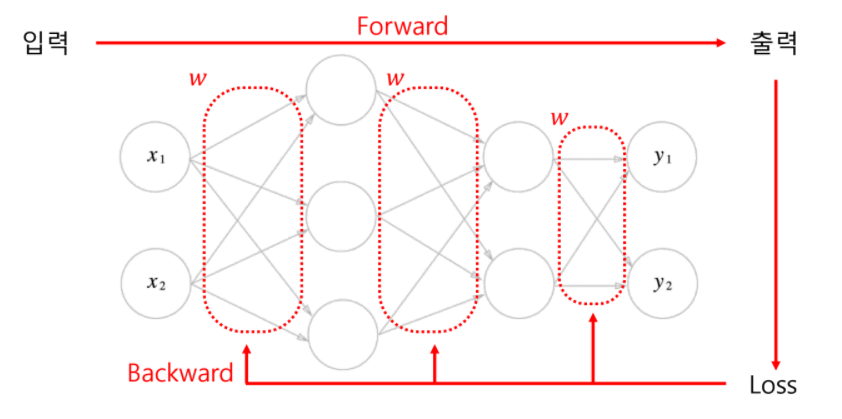
Gradiend decent(경사 하강법) = Back propagation의 수단
임의의 한 지점으로부터 시작해 loss가 줄어드는 방향으로 w(weights = parameters)들을 갱신하는 방법
loss가 더이상 감소하지 않는 시점까지 w를 음의 기울기 방향(-)으로 조금씩 움직이는 것을 여러 번 반복
목적지 : loss의 최소 지점
목적지의 방향 : 미분을 이용
목적지의 방향으로 얼마만큼 이동해야 하는가? : Learning rate
learning rate가 작으면 : 최저점을 찾는 과정이 매우 더딤
learning rate가 크면 : 최저점을 찾지 못할 수 있음
따라서 적절한 learning rate가 이상적이다!

-Gradient decent의 수단 = chain rule
Forward 과정을 통해 나온 Loss에 각 w들이 끼친 영향을 알기 위해서는 전체 loss를 각각의 w로 편미분 해야한다.
하지만 loss를 직접적으로 w에 대해 미분하기란 쉽지 않다.

단층 퍼셉트론의 경우 MSE loss는 다음과 같다.
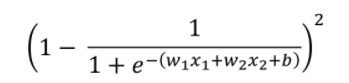
입,출력이 조금 더 많거나, 퍼셉트론이 다층일 경우 계산은 더 복잡해진다. > 첫번째 인공지능의 겨울을 가져온 이유 중 하나
해결법 : Chain rule 을 이용한 Back propagation
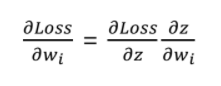
Batch learning(Epoch learning)
전체 훈련 데이터를 사용 > 장점 : 전제 데이터를 한번에 훑고 좋은 데이터를 이용 & 단점 : 모든 데이터를 다 봐주어 야 하므로 시간이 길어진다.
대규모 데이터 셋에 적용하기 힘듦
데이터 구성이 항상 같기 때문에 local minima에 빠질 위험이 있다.
특별한 경우가 아니라면 이 방식으로 훈련시키지 않는다.
Mini batch
몇 개의 샘플을 하나의 소규모 집합 단위로 가중치를 업데이트(SGD)
복수의 샘플을 묶은 작은 집합
epoch : 전체 데이터셋
batch size : mini batch의 크기
iterations : batch size를 반복한 횟수

autograd
딥러닝 모델은 매우 많은 연산을 통해 결과를 도출한다.
하지만 그 연산들은 잘게 쪼개면 더하기, 곱하기, 나누기, 지수연산으로 이루어진다.
chain rule 은 복잡한 연산을 기본 연산으로 나누어 미분한다.
결국 더하기 곱하기 나누기의 미분과정만 알면 목적인 loss를 w에 미분한 값을 얻을 수 있다.
pytorch에서는 이러한 방식으로 backpropagate하는 방법을 autograd라 한다.
Optimization
Back propagation을 통해 weights(=parameters)을 업데이트 시키는 방법
1.Stochastic Gradient decent(SGD)
batch learning과는 달리 샘플 일부만을 사용해 파라미터를 업데이트하는 방법
빠른 학습 가능, local minima에 빠질 위험이 적다
노이즈 데이터로 인해 변동이 크다
Epoch마다 무작위로 샘플을 선택하면 그 효과를 극대화할 수 있고 때문에 stochastic Gradient decent라 부름

2.AdaGrad
개별 가중치에 적응적으로 (adaptive) 학습률을 조정하면서 학습을진행
현재까지 따라서 많이 갱신된 가중치는 학습률을 낮아짐
즉 학습률 감소가 개별 가중치마다 다르게 적용

3.RMSprop
AdaGrad의 단점을 해결하기 위한 방법
AdaGrad의 식에서 gradient의 제곱값을 더하는 방식이 아니라 지수 평균으로 대체
Gradient가 무한정 커지는 것을 방지
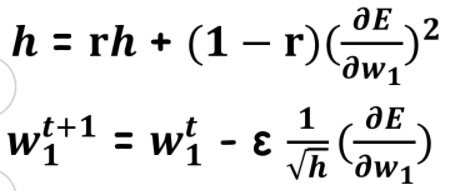
4.Momentum
가중치의 업데이트 값에 이전 업데이트 값의 일정비율을 더해줌
즉 Gradient decent를 통해 이동하는 과정에 관성을 주는것
Adam : AdaGrad와 Momentum을 융합한 기법
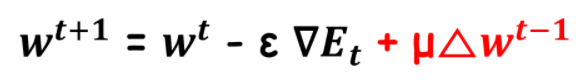
'AI > Deep Learning' 카테고리의 다른 글
| 4. CNN 기초 (0) | 2022.01.21 |
|---|---|
| 3. 딥러닝 학습 방법론 (0) | 2022.01.21 |
| 딥러닝 학습방법론 (0) | 2021.11.23 |
| 딥러닝 기초이론 학습의 과정-2 : Loss and Gradient (0) | 2021.11.23 |
| 1. 딥러닝 학습 기초 (0) | 2021.11.22 |




