Kim Seon Deok
딥러닝 기초이론 학습의 과정-2 : Loss and Gradient 본문
학습의 과정
2.Loss and Gradient = Backward propagation = 역전파
Loss function
-Feed Forward를 통해 출력으로 나온 데이터가 실제 정답과 얼마나 차이가 나는지를 나타냄
-딥러닝 네트워크가 어떤 방향으로 학습되어야 하는지 학습의 방향을 설정하는 아주 중요한 부분
-이 Loss Func의 결과값을 토대로 네트워크의 Weight들이 업데이트 됨
-학습을 거듭 반복하면서 Loss Function값은 작아진다.
회귀(Regression)문제 >> Mean Squared Error(평균 제곱 오차)
분류(Classification)문제 >> Cross Entropy(교차 엔트로피 오차)
-정답일 때의 출력이 전체 값을 결정
-실제 정답이 아닌 요소에 대해 잘못 예측한 값은 Loss에 포함돼지 않아 계산의 효율성이 올라간다.
-cross entropy : 서로 다른 두 상태의 정보량 차이를 나타내는 척도


* Entropy
정보이론 관점에서 얼만큼의 정보를 갖고 있는지 정량적으로 표현하기 위해 사용하는 척도
너무 뻔해서 결과가 예측돼는 상황 > 엔트로피가 작다
결과를 예측할 수 없는 상황 > 엔트로피가 크다
Back propagaton
-출력과 Loss는 w들의 결과로 나온 값
-Loss를 바탕으로 각각의 w 하나하나가 얼마나 영향을 주었는지 알아내고, 좀 더 적절한 방향으로 w들을 변경해 나가는 것
-학습의 목표 : 가능한 작은 loss값을 갖는 w를 찾는것
-Gradient Decent를 이용해 w를 찾음
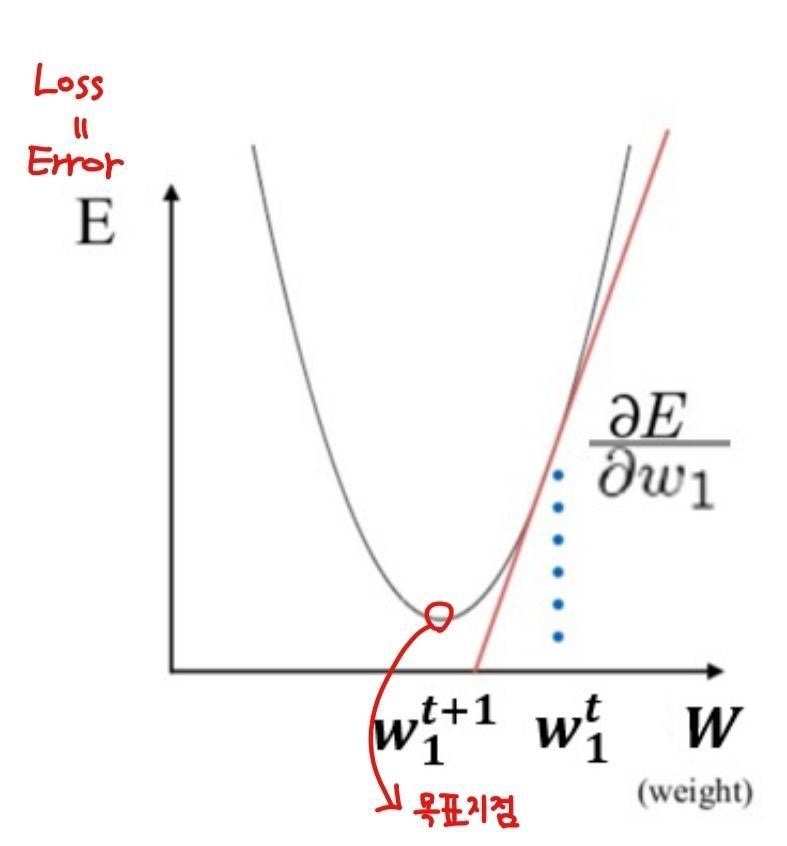
Gradient Decent(경사하강법)
-임의의 한 지점으로부터 시작해, loss가 줄어드는 방향으로 w들을 갱신하는 방법
-목표 : Loss의 최소지점
-목표의 방향 : 미분을 이용
Forward과정을 통해 나온 Loss에 각 w들이 끼친 영향을 알기 위해서는 전체 Loss를 각각의 w로 편미분해야 한다.
하지만 loss를 직접적으로 w에 대해 미분하기란 쉽지 않다.
입출력이 조금 더 많거나, 퍼셉트론이 다층일 경우 계산은 더 복잡해진다. >> 인공지능의 첫번째 겨울을 가져옴
* Chain rule을 이용
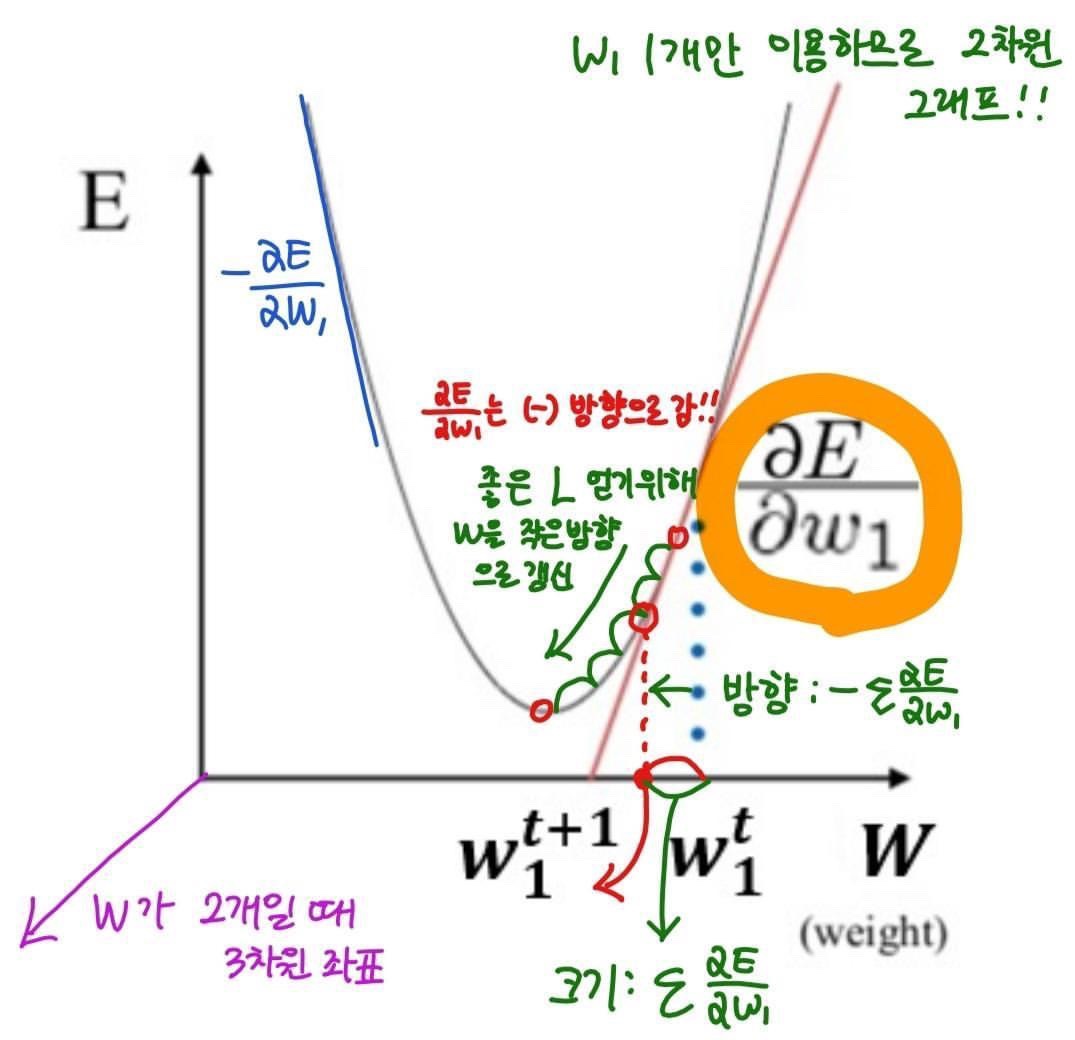
-목표의 방향으로 움직여야 하는 정도: Learning rate == 보폭
-미분갑 X learning rate 만큼 w들을 수정
-loss가 더이상 감소하지 않는 시점까지 w를 음의 기울기 방향(-)으로 조금씩 움직이는 것을 여러 번 반복
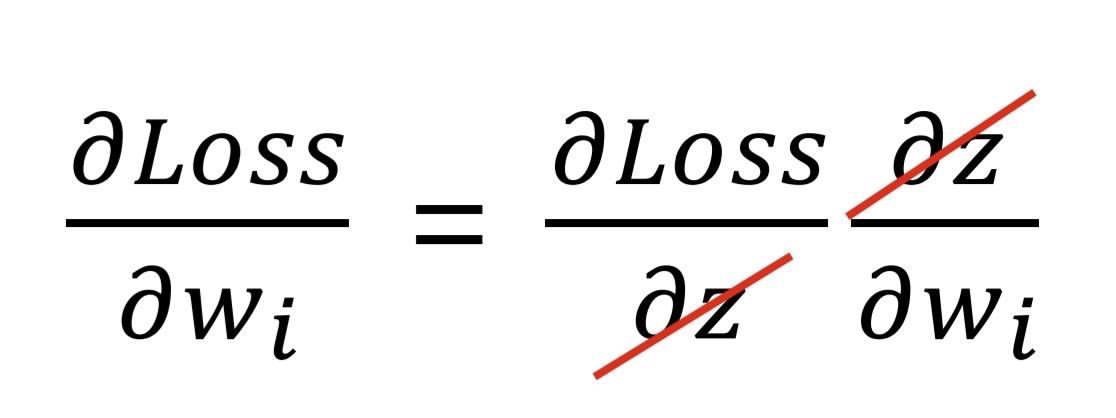
* learning rate
작으면 최저점을 찾는 과정이 매우 더딤
크면 최저점을 못 찾을 수 있음
따라서 learning rate가 적절한 값이 이상적이다!

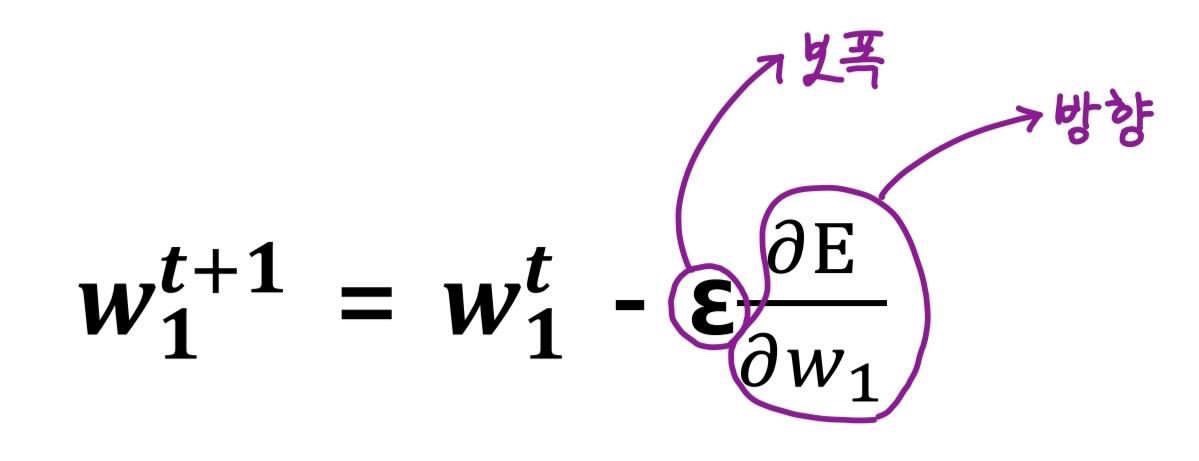

Autograd
딥러닝 모델(네트워크)은 매우 많은 연산을 통해 결과를 도출한다. 하지만 그 연산들을 잘게 쪼개보면 더하기, 곱하기, 나누기, 지수연산으로 이루어진다.
chain rule은 복잡한 연산을 기본연산으로 나누어 미분한다.
+, *, /으로 backpopagatie를 진행하는 것을 auograd라고 한다.
3.Update
optimization
Back propagation을 통해 weights를 업데이트 시키는 방법
1.Stochastic Gradient decent(SGD)
-Batch learning과는 달리 샘플 일부만을 사용해 파라미터를 업데이트 하는 방법
-빠른 학습 가능, local minima에 빠질 위험이 적음
-노이즈 데이터로 인해 변동이 큼
-Epoch마다 무작위로 샘플을 선택하면 효과를 극대화 할 수 있다.
2.AdaGrad
-개별 가중치에 적응적으로(adaptive) 학습률을 조정하면서 학습을 진행
-현재까지 따라서 많이 갱신된 가중치는 학습률을 낮춤
-학습률 감소가 개별 가중치마다 다르게 적용
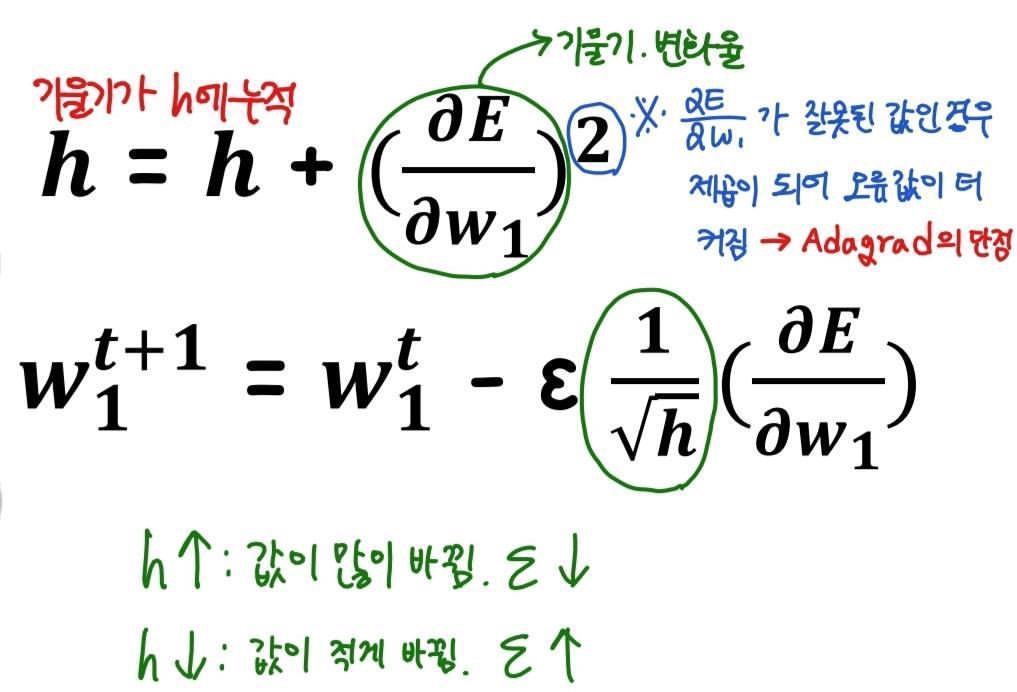
3.RMSProp
-AdaGrad의 단점을 해결하기 위한 방법
-AdaGrad의 식에서 Gradient의 제곱값을 더하는 방식이 아니라 지수평균으로 대체해 Gradient가 무한정 커지는 것을 방지
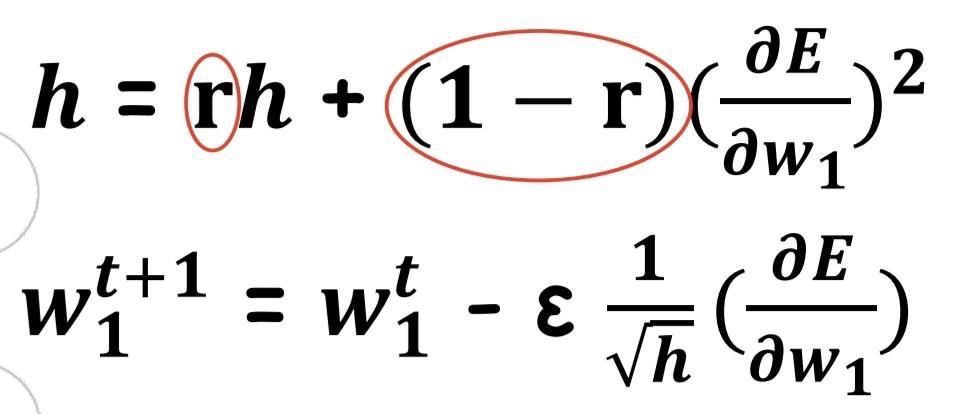
4.Momentum
-가중치의 업데이트 값에 이전 업데이트 값의 일정 비율을 더해줌
-Gradient decent를 통해 이동하는 과정에 관성을 줌
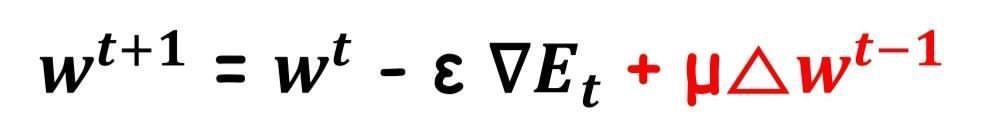
5.Adam
AdaGrad와 Momentum을 결합한 기법
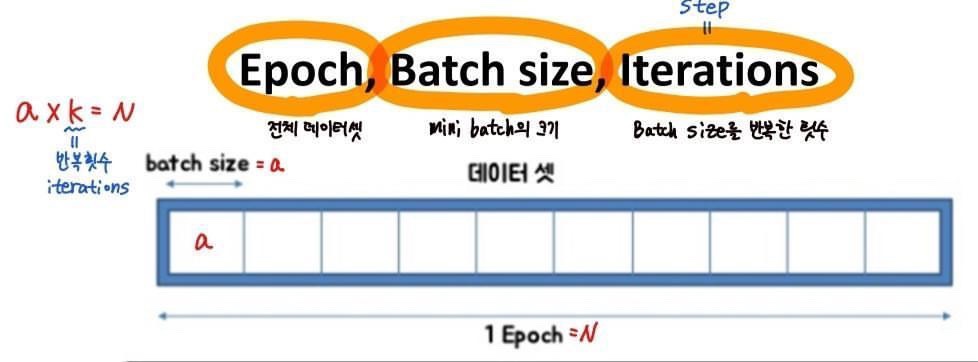
Batch Learning(Epoch Learning)
-전체 훈련 데이터를 사용
-전체 데이터를 한번에 훑고 좋은 데이터를 이용
-모든 데이터를 다 봐주어야 하므로 학습시간이 길어짐
-대규모 데이터 셋에 적용하기 힘듦
-데이터 구성이 항상 같기 때문에 local minima (지역 최소값, 데이터 구성이 같아 컴퓨터가 편법을사용해 loss가 작은 값으로 학습하여, 더 작은 loss를 찾으려 하지 않음) 에 빠질 위험이 있음
Mini-Batch
-복수의 샘플을 묶은 작은 집합
-몇 개의 샘플을 하나의 소규모 집합 단위로 가중치를 업데이트(SGD)

'AI > Deep Learning' 카테고리의 다른 글
| 1. Back propagation (0) | 2022.01.21 |
|---|---|
| 딥러닝 학습방법론 (0) | 2021.11.23 |
| 1. 딥러닝 학습 기초 (0) | 2021.11.22 |
| LSTM (0) | 2021.11.20 |
| RNN 기초 (0) | 2021.11.19 |




