Kim Seon Deok
밑바닥부터 시작하는 딥러닝 1 : 6장 - 학습관련 기술들 본문
6-1 매개변수 갱신
신경망 학습의 목적 : loss function의 값을 가능한 한 낮추는 매개변수를 찾는 것
최적화(optimization) : 매개변수의 최적값을 찾음
optimizer : 최적화를 행하는 자. 매개변수를 갱신
1. 확률적 경사 하강법(SGD)
매개변수의 기울기를 구해 가장 크게 기울어진 방향으로 매개변수 값을 갱신하는 일을 반복해 점점 최적의 값에 다다름
w : 가중치 매개변수, n : 학습률, aL/aw : 기울기(손실함수)


심하게 굽어진 움직임
비등방성 함수(방향에 따라 기울기가 달라짐.) - 탐색 경로가 비효율적
기울어진 방향이 본래의 최솟값과 다른 방향을 가리킴
2.모멘텀(Momentum)
기울기 방향으로 힘을 받아 물체가 가속된다.


v : 속도, av: 물체가 아무런 힘을 받지 않을 때 서서히 하강시킴
SGD보다 지그재그 경로가 덜하다.
x축 힘은 아주 작지만 방향은 변하지 x - 한 방향으로 일정하게 가속
y축 힘은 크지만 위아래로 번갈아 받아 상충 - y축 방향속도 안정적이지x
*학습률 감소
학습을 진행하면서 학습률을 점차 줄여나가는 방법(크게 학습하다 조금씩 작게 학습)
학습률을 낮추는 법 : 매개변수 '전체'의 학습률 값을 일괄적으로 낮춤
3.AdaGrad

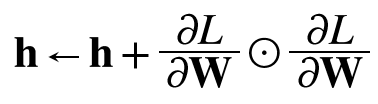
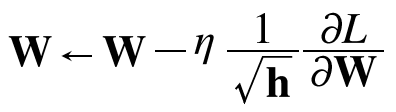
1/루트h : 학습률 조정
기존 기울기값을 제곱해 계속 더함
개별 매개변수에 적응적으로 학습률을 조정하면서 학습을 진행
-y축 방향은 기울기가 커서 처음에는 크게 움직이지만, 큰 움직임에 비례해 갱신정도도 큰 폭으로 작아진다.
>> y축 방향으로 갱신강도 약해지고, 지그재그 움직임 줄어듦.
-많이 움직인, 크게 갱신된 원소는 학습률 낮아짐 >> 학습률 감소가 원소마다 다르게 적용됨
4.RMSProp
과거의 모든 기울기를 균일하게 더해가는 것이 아니라, 먼 과거의 기울기는 잊고 새로운 기울기 정보를 크게 반영 - 지수이동 평균(과거 기울기의 반영규모 기하급수적으로 감소)
5.Adam : Momentum & AdaGrad
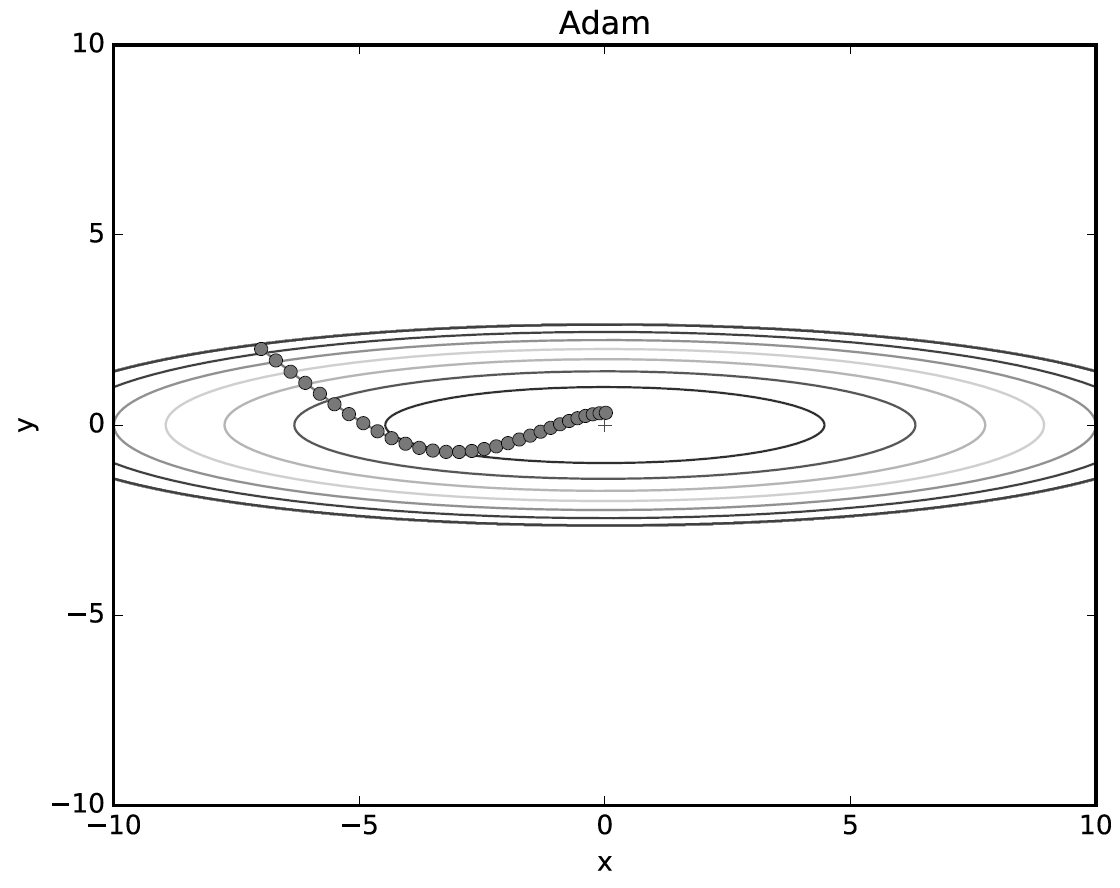
하이퍼 파라미터의 '편향보정'이 진행된다.
모멘텀과 비슷한 패턴인데, 모멘텀 때보다 좌우 흔들림이 적다
6-2. 가중치 초깃값
가중치 감소 : 가중치 매개변수 값이 작아지도록 학습하는 방법 > 가중치 값이 작아져 오버피팅 일어나지 않는다.
*가중치 초깃값을 0으로 하면 안되는 이유?
가중치를 균일한 값으로 설정해서는 안된다. 오차역전파법에서 모든 가중치 값이 똑같이 갱신되기 때문이다.
순전파) 입력가중치 = 0 > 두번째 층 뉴런에 모두 균일한 값 전달 > 모두 똑같이 갱신
같은 초깃값에서 시작하고 갱신을 거쳐도 여전히 같은 값을 유지
>> 가중치가 고르게 되어버리는 상황을 막으려면 초깃값을 무작위로 설정해야 한다.
가중치 초깃값에 따른 은닉층 활성화 값들의 변화
1. 표준편차 : 1
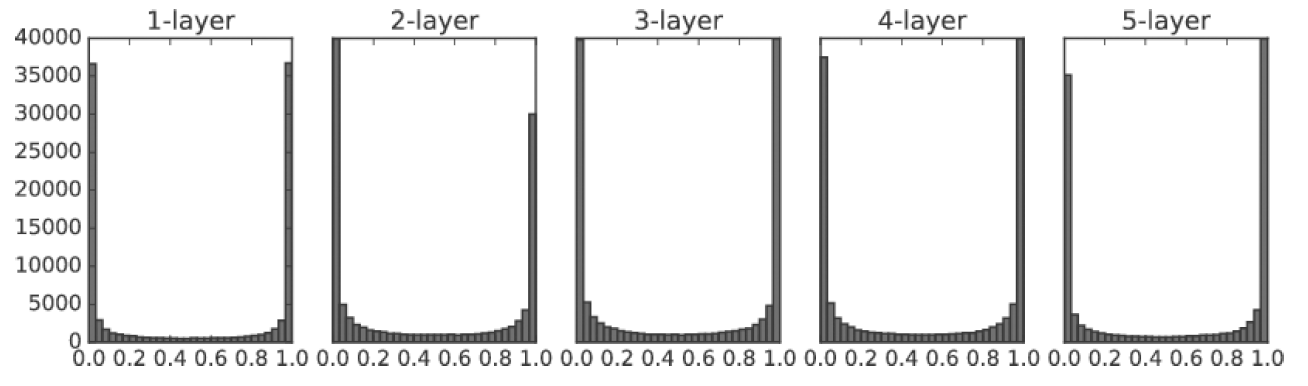
각 층의 활성화들이 0,1에 치우침
sigmoid function은 출력이 0 또는 1 에 가까워지면 미분이 0에 다가감
>> 0과 1에 치우쳐 분포되면 역전파 기울기 값이 점점 작아지다 사라짐
2. 표준편자 : 0.5
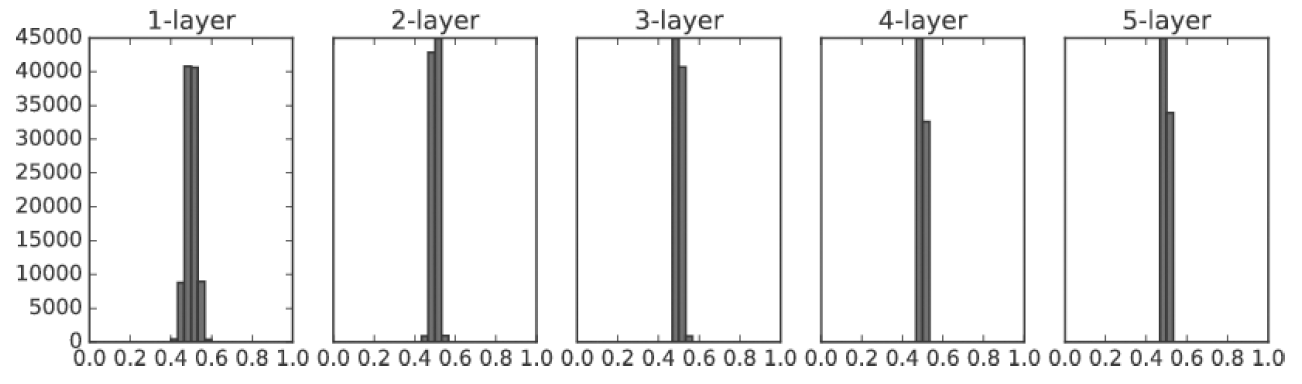
그래도 활성화 값이 한 곳에 치우침
>> 뉴런을 여러개 둔 의미가 사라짐
결론 : 활성화 값이 치우치면 기울기 소실 문제, 표현력을 제한한다는 점에서 문제가 된다.
각 층의 활성화 값은 적당히 고루 분포해야 한다.
* 활성화 값 치우침 해결법(각 층의 활성화 값들을 광범위하게 분포시킬 목적)
1. Xavier 초깃값(활성화 함수가 선형인 것을 전제로 Sigmoid, tanh함수 사용)
앞 층 노드가 n개라면 표준편차가 1/루트n 인 분포를 사용
- 앞 층 노드가 많을 수록 대상 노드의 초깃값으로 설정하는 가중치가 좁게 펴짐
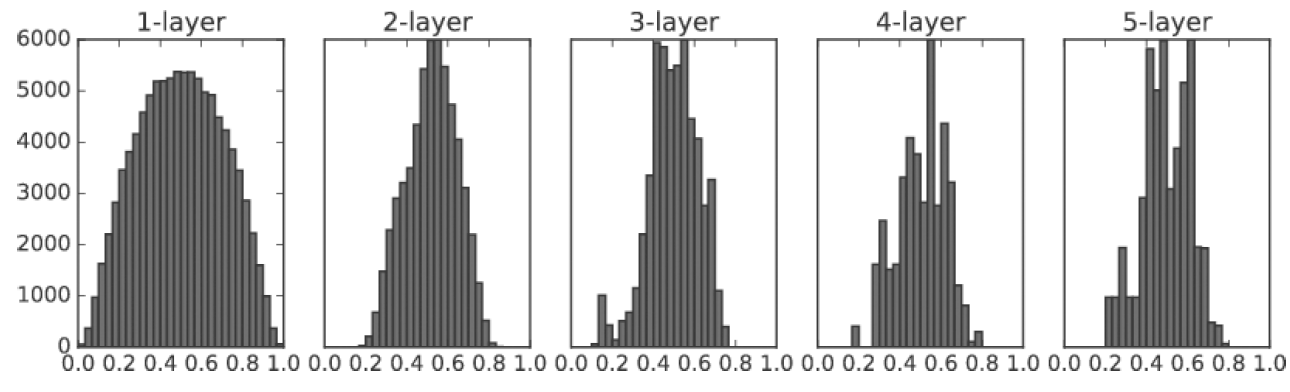
sigmoid function의 표현력에도 제한받지 않고 학습이 효율적으로 이루어짐.
sigmoid, tanh 함수는 좌우 대칭이라 중앙 부근이 선형이다.
2.He 초깃값
앞 층 노드가 n개일 때, 표준편차가 루트(2/n)인 정규분포를 사용
ReLU는 음의 영역이 0이기 때문에 더 넓게 분포시키기 위해 2배의 계수를 사용
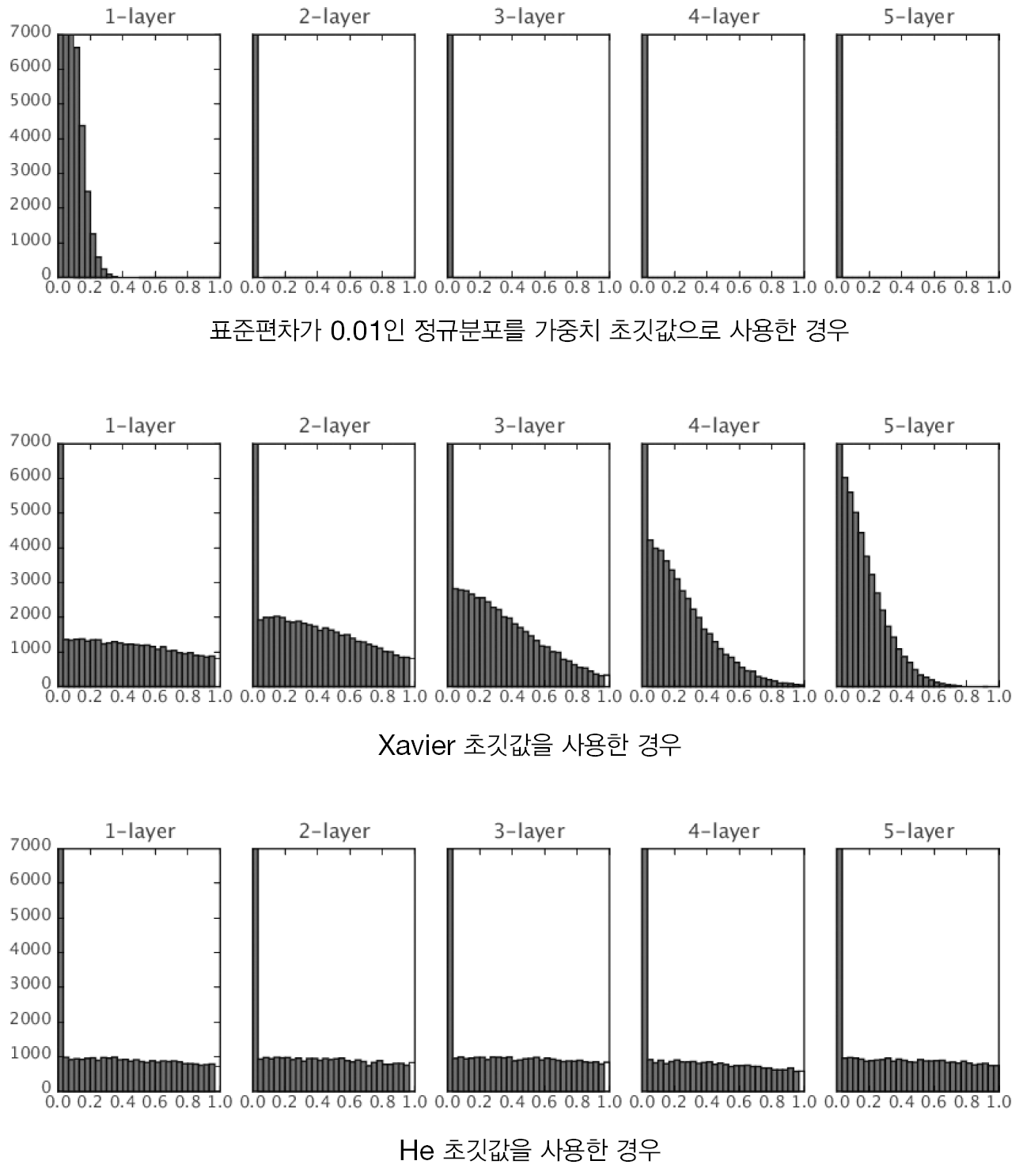
6-3. 배치 정규화(Batch-Normalization)
각 층이 활성화를 적당히 퍼뜨리도록 강제
배치 정규화의 장점
1. 학습을 빨리 진행할 수 있다.
2. 초깃값에 크게 의존하지 않는다.
3. 오버피팅을 억제
분포 평균이 0, 분산이 1 이 되도록 미니배치를 단위로 정규화
6-4. 바른 학습을 위해
오버피팅 : 신경망이 훈련 데이터에만 지나치게 적응하여 그 외의 데이터에는 대응하지 못하는 상태
-매개변수가 많고 표현력 높은 모델
-훈련 데이터가 적음
가중치 감소 : 학습 중 큰 가중치에 대해선 그에 상응하는 큰 페널티를 부과해 오버피팅을 억제
Dropout : 뉴런을 임의로 삭제하면서 학습하는 방법
앙상블 학습 : 개별적으로 학습시킨 여러 모델의 출력을 평균내어 추론
6-5. 적절한 하이퍼 파라미터 값 찾기
하이퍼 파라미터의 성능을 평가할 땐 test data를 사용하면 x.
하이퍼 파라미터 값의 '좋음'을 test data로 확인하므로 하이퍼 파라미터 값이 시험데이터에만 적합하도록 조정되어 범용성능이 떨어지게 된다.
validation data : 하이퍼 파라미터 조정용 데이터, 하리퍼 파라미터 성능 평가
train data : 매개변수(가중치, 편향) 학습
test data : 범용성능 확인
하이퍼 파라미터 최적화
'최적값'이 존재하는 범위를 조금씩 줄여나감
1.대략적인 범위 설정(log scale)
2.무작위로 하이퍼파라미터 값 샘플링
3.정확도 평가
미니배치 학습 구현
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
(x_train, t_train), (x_test, t_test) = load_mnist(normalize = True, one_hot_encoding = True)
train_loss_list = []
# 하이퍼파라미터
iters_num = 10000 # 반복횟수
train_size = x_train.shape[0]
batch_size = 100 # 미니 배치 크기
learning_rate = 0.1
network = TwoLayerNet(input_size = 784, hidden_size = 50, output_size = 10)
for i in range(iters_num):
# 미니배치 획득
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
grad = network.numerical_gradient(x_batch, t_batch)
# grad = network.gradient(x_batch, t_batch) # 성능 개선판 !
# 매개변수 갱신
for key in ('w1','b1','w2','b2'):
network.params[key] -= learning_rate * grad[key]
# 학습 경과 기록
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 시험 데이터로 평가하기
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
(x_train, t_train),(x_test,t_test) = load_mnist(normalize = True, one_hot_label = True)
network = TwoLayerNet(input_size = 784, hidden_size = 50, output_size = 10)
# 하이퍼 파라미터
iters_num = 10000 # 반복 횟수를 적절히 설정
train_size = x_train.shape[0]
batch_size = 100 # 미니배치 크기
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list =[]
# 1에폭 당 반복 수
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
# 미니배치 획득
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
grad = network.numerical_gradient(x_batch, t_batch)
# grad = network.gradient(x_batch, t_batch) # 성능 개선판 !
# 매개변수 갱신
for key in ('w1','b1','w2','b2'):
network.params[key] -= learning_rate * grad[key]
# 학습 경과 기록
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 1에폭 당 정확도 계산
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + " , " + str(test_acc))'AI > Deep Learning' 카테고리의 다른 글
| 밑바닥부터 시작하는 딥러닝 2 : 2장 - 자연어와 단어의 분산 표현 (0) | 2022.03.09 |
|---|---|
| 밑바닥부터 시작하는 딥러닝 1 : 7장 합성곱 신경망(CNN) (0) | 2022.03.08 |
| 밑바닥부터 시작하는 딥러닝 1 : 5장 - 오차역전파법 (0) | 2022.03.08 |
| 밑바닥부터 시작하는 딥러닝 1 : 4장 - 신경망 학습 (0) | 2022.03.08 |
| 밑바닥부터 시작하는 딥러닝 1 - 3장 : 신경망 (0) | 2022.03.08 |




