Kim Seon Deok
9 - 2 이진 트리와 이진 검색 트리 본문
이진 트리(binary tree)
노드가 왼쪽자식과 오른쪽 자식 만을 갖는 트리
왼쪽 자식과 오른쪽 자식을 구분
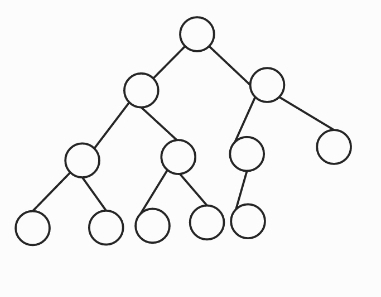
완전 이진 트리
루트부터 아래쪽 레벨로 노드가 가득 차있고, 같은 레벨 안에서 왼쪽부터 오른쪽으로 노드가 채워져있는 이진트리.
높이가 k인 완전 이진 트리가 가질 수 있는 노드의 수는 최대 2(k+1)-1개 이므로, n개의 노드를 저장할 수 있는 완전 이진 트리의 높이는 logn입니다.
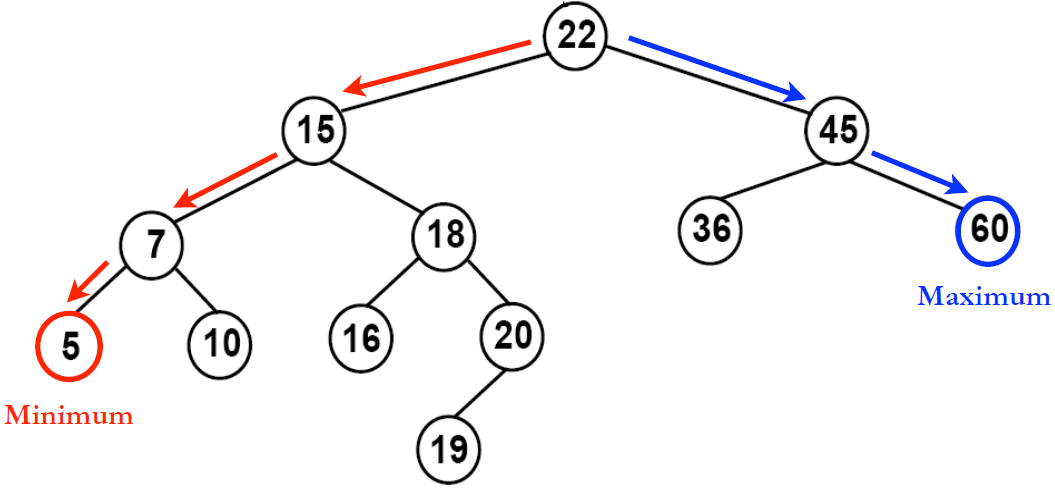
이진 검색 트리
왼쪽 서브트리 노드의 키값은 자신의 노드 키값보다 작아야 합니다.
오른쪽 서브트리 노드의 키값은 자신의 노드 키값보다 커야 합니다.
키값이 같은 노드는 복수로 존재하지 않습니다.
-구조가 단순하다.
-중위 순회의 깊이 우선 검색을 통해 노드값을 오름차순으로 얻을 수 있다.
-이진검색과 비슷한 방식으로 아주 빠르게 검색할 수 있다.
-노드를 삽입하기 쉽다.
# 이진 검색 트리 구현하기
from __future__ import annotations
from typing import Any, type
class Node:
"""이진 검색 트리의 노드"""
def __init__(self, key:Any, value: Any, left: Node = None,
right: Node=None):
"""생성자"""
self.key = key # 키
self.value = value # 값
self.left = left # 왼쪽 포인터
self.right = right # 오른쪽 포인터
class BinarySearchTree:
"""이진 검색 트리"""
def __init__(self):
"""초기회"""
self.root = None # 루트
def search(self, key:Any) -> Any:
"""키가 key인 노드를 검색"""
p = self.root # 루트에 주목
while True:
if p is None: # 더 이상 진행할 수 없으면
return None
if key == p.key: # key와 노드 p의 키가 같으면
return p.value # 검색성공
elif key < p.key: # key쪽이 작으면
p = p.left # 왼쪽 서브트리에서 검색
else: # key쪽이 크면
p = p.right # 오른쪽 서브트리에서 검색
def add(self,key:Any,value:Any) -> bool:
"""키가 key이고 값이 value인 노드를 삽입"""
def add_node(node:Node, key:Any, value:Any) -> None:
"""node를 루트로 하는 서브트리에 키가 key이고 값이 value인 노드를 삽입"""
if key == node.key:
return False # key가 이진 검색 트리에 이미 존재
elif key < node.key:
if node.left is None:
node.left = Node(key, value, None, None)
else:
add_node(node.left, key, value) # 왼쪽 노드에 삽입
else:
if node.right is None:
node.right = Node(key, value, None, None)
else:
add_node(node.right, key, value) # 오른쪽 노드에 삽입
return True
if self.root is None: # root가 None일 때
self.root = Node(key, value, None, None)
return True
else:
return add_node(self.root, key, value)
def remove(self, key:Any) -> bool:
"""키가 key인 노드를 삭제"""
p = self.root # 스캔 중인 노드
parent = None # 스캔 중인 노드의 부모 노드
is_left_child = True # p는 parent의 왼쪽 자식 노드인지 확인
while True:
if p is None: # 더 이상 진행할 수 없으면
return False # 그 키는 존재하지 않음
if key == p.key: # key와 노드 p의 키가 같으면
break # 검색 성공
else:
parent = p # 가지를 내려가기 전에 부모를 설정
if key < p.key: # key쪽이 작으면
is_left_child = True # 여기서 내려가는 것은 왼쪽 자식
p = p.left # 왼쪽 서브트리에서 검색
else: # key쪽이 크면
is_left_child = False # 여기서 내려가는 것은 오른쪽 자식
p = p.right # 오른쪽 서브트리에서 검색
if p.left is None: #p에 왼쪽 자식이 없으면
if p is self.root:
self.root = p.right
elif is_left_child:
parent.left = p.right #부모의 왼쪽 포인터가 오른쪽 자식을 가리킴
else:
parent.right = p.right # 부모의 오른쪽 포인터가 오른쪽 자식을 가리킴
elif p.right is None: # p에 오른쪽 자식이 없으면
if p is self.root:
self.root = p.left
elif is_left_child:
parent.left = p.left #부모의 왼쪽 포인터가 왼쪽 자식을 가리킴
else:
parent.right = p.left # 부모의 오른쪽 포인터가 왼쪽 자식을 가리킴
else:
parent = p
left = p.left #서브트리 안에서 가장 큰 노드
is_left_child = True
while left.right is not None: #가장 큰 노드 left를 검색
parent = left
left = left.right
is_left_child = False
p.key = left.key #left의 키를 p로 이동
p.value = left.value #left의 데이터를 p로 이동
if is_left_child:
parent.left = left.left # left를 삭제
else:
parent.right = left.right # left를 삭제
return True
def dump(self) -> None:
"""덤프(모든 노드를 키의 오름차순으로 출력)"""
def print_subtree(node:Node):
"""node를 루트로 하는 서브트리의 노드를 키의 오름차순으로 출력"""
if node is not None:
print_subtree(node.left) #왼쪽 서브트리를 오름차순으로 출력
print(f'{node.key} {node.value}') # node를 출력
print_subtree(node.right) #오른쪽 서브트리를 오름차순으로 출력
print_subtree(self.root)
def min_key(self) -> Any:
"""가장 작은 키"""
if self.root is None:
return None
p = self.root
while p.left is not None:
p = p.left
return p.key
def max_key(self) -> Any:
"""가장 큰 키"""
if self.root is None:
return None
p = self.root
while p.right is not None:
p = p.right
return p.key1.키값으로 노드를 검색하는 search()함수
루트에 주목 > 주목하는 노드 p
p가 None이면 검색을 실패하고 종료
key = p : 검색을 성공하고 종료
key < p : 주목노드를 왼쪽 자식 노드로 옮김
key > p : 주목 노드를 오른쪽 자식 노드로 옮김
2.노드를 삽입하는 add()함수
노드를 삽입한 뒤 트리의 형태가 이진 검색 트리의 조건을 유지해야 한다.
루트에 주목 > 주목하는 노드 node
key = node : 삽입을 실패하고 종료
key < node : 왼쪽 자식 노드가 없으면 노드를 그 자리에 삽입하고 종료
왼쪽 자식 노드가 있으면 주목노드를 자식노드로 옮김
key > node : 오른쪽 자식 노드가 없으면 노드를 그 자리에 삽입하고 종료
오른쪽 자식 노드가 있으면 주목노드를 자식노드로 옮김
3.노드를 삭제하는 remove()함수
3-1.자식노드가 없는 노드를 삭제하는 경우
삭제할 노드가 부모 노드의 왼쪽 자식이면, 부모의 왼쪽 포인터를 None
삭제할 노드가 부모 노드의 오른쪽 자식이면, 부모의 오른쪽 포인터를 None
3-2.자식노드가 1개인 노드를 삭제하는 경우
삭제할 노드가 부모 노드의 왼쪽 자식인 경우 : 부모의 왼쪽 포인터가 삭제할 노드의 자식을 가리키도록 업데이트
삭제할 노드가 부모 노드의 오른쪽 자식인 경우 : 부모의 오른쪽 포인터가 삭제할 노드의 자식을 가리키도록 업데이트
3-3.자식노드가 2개인 노드를 삭제하는 경우
삭제할 노드의 왼쪽 서브트리에서 키값이 가장 큰 노드를 검색
검색한 노드를 삭제 위치로 옮김.
옮긴 노드를 삭제. 이 때 옮긴 노드에 자식이 없으면 > 3-1 방식, 자식이 1개만 있으면 > 3-2 방식

균형 검색 트리
이진 검색 트리는 키의 오름차순으로 노드가 삽입되면 트리의 높이가 깊어지는 단점이 있다.
직선모양의 트리가 되면, 실제로 선형 리스트처럼 되어 아주 빠른 검색을 수행할 수 없다.
높이를O(logn)으로 제한하여 고안된 검색트리이다.
'python > Data Structure' 카테고리의 다른 글
| 9 - 1 트리구조 (0) | 2022.02.01 |
|---|---|
| 7-1 브루트 포스법 & 7 - 2 KMP법 7-3 보이어-무어법 (0) | 2022.01.28 |
| 6 - 8 힙 정렬 & 6 - 9 도수 정렬 (0) | 2022.01.27 |
| 6 - 6 퀵 정렬 & 6-7 병합정렬 (0) | 2022.01.26 |
| chapter 6 -3 단순 선택 정렬, 6 - 4 단순 삽입 정렬, 6 - 5 셸 정렬 (0) | 2022.01.22 |




